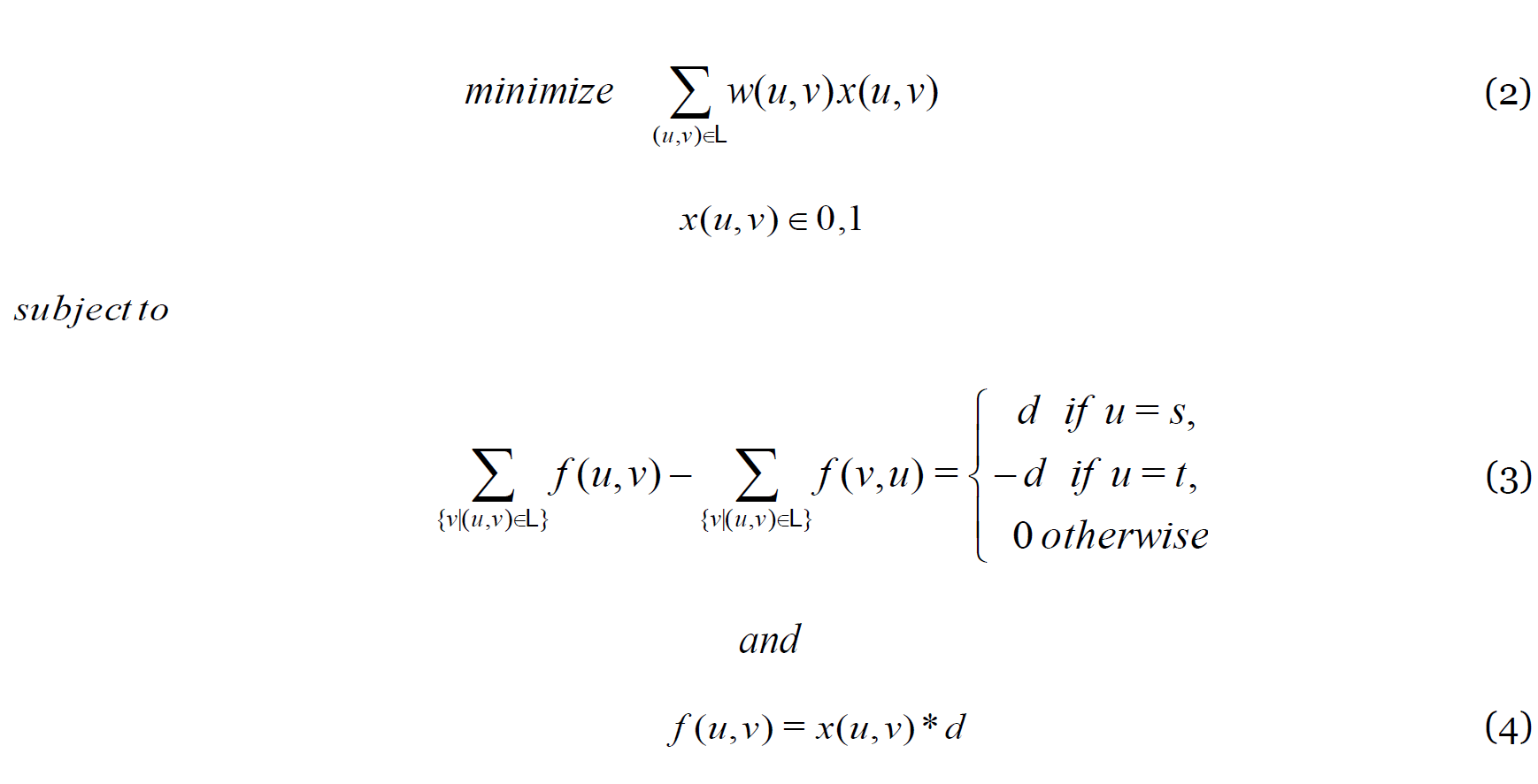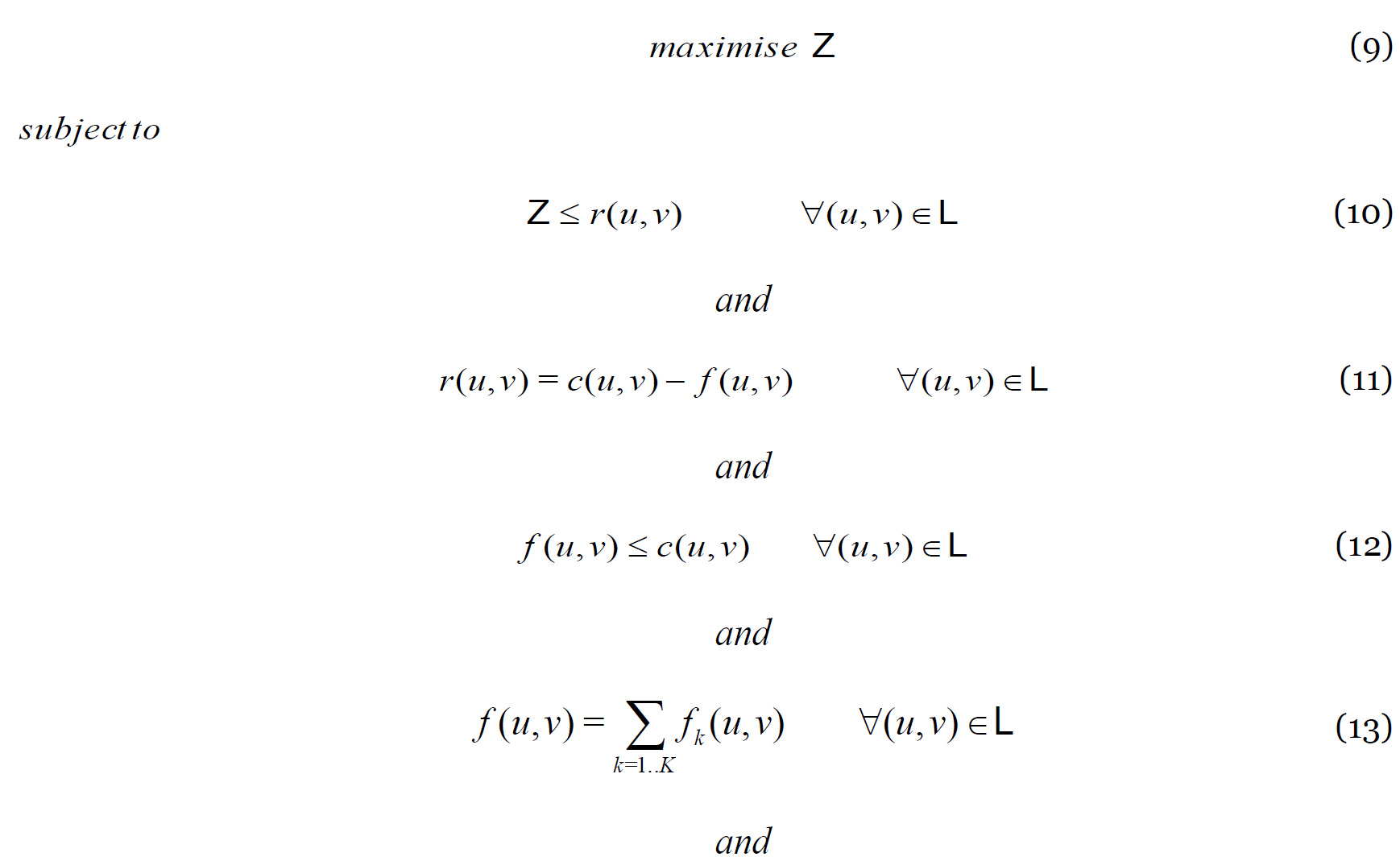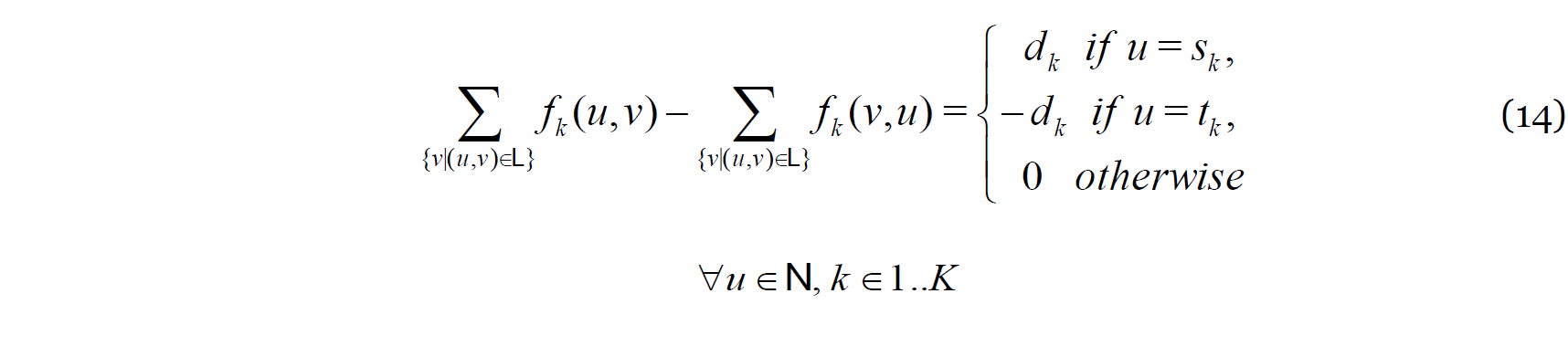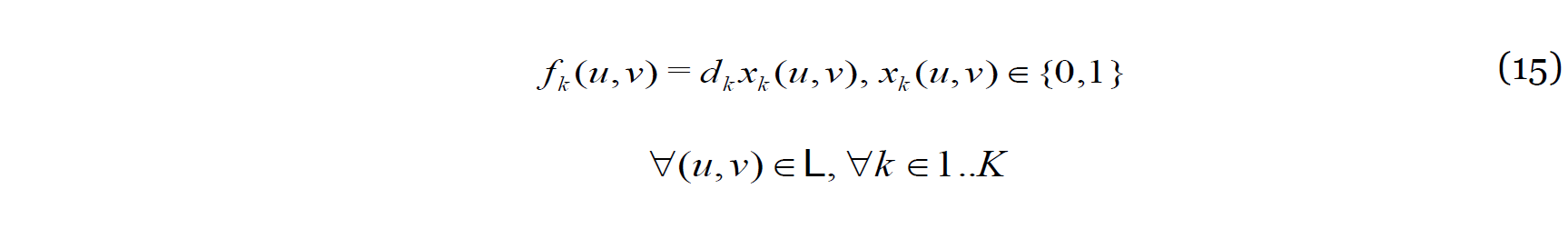1. Introduction

Software Defined Networking (SDN) aims to improve network programmability, simplify network management and enhance network operation. It represents a paradigm shift in networking that decouples the control plane from the data plane, and places the control of the system in a logically centralised node, called SDN controller. Consequently, the SDN controller has a global view of the network, which facilitates the rapid development and deployment of new network services and applications (McKeown 2009). The SDN architecture consists of three layers, i.e. infrastructure, control and application layer. The control layer (SDN controller) provides key abstractions and network services for the application layer through the northbound interface. There is a range of SDN northbound interfaces with various functionalities, but no dominant standard has evolved so far (Kreutz et al. 2015).

Today's networking environment necessitates using various Quality of Service (QoS) routing and Traffic Engineering (TE) techniques to optimise the traffic flow for different applications and traffic types, e.g. voice and video. The implementation of these QoS routing and TE applications, which can be complex, is not readily supported by current northbound interfaces. Despite the vital importance of these applications in networking, they still require a lot of low-level effort and a high degree of skills in order to be implemented in SDN.

In order to address this gap, this paper introduces a new SDN northbound interface. This interface is based on Constraint-Programming (CP) techniques to provide Software-defined Constrained Optimal Routing (SCOR). The main idea behind using CP methods in SCOR is to provide a level of abstraction and hide the complexity from the user.

In CP, users only state the constraints that the solution should have, and do not specify a step-by-step solution of the problem, as in the case of procedural programming. In other words, in CP users are only concerned with expressing or declaring the problem, and not with its solution. The solution is provided by a powerful general-purpose CP solver. SCOR provides an interface for expressing QoS routing applications, consisting of nine basic building blocks, i.e. predicates. We show in this paper that this interface is able to model both simple and complex QoS routing problems, in a very simple and compact manner. The scalability of SCOR is also evaluated through a number of example applications and a number of experiments.

SCOR is explained after a brief background in Section 2, and a short review on related works in Section 3. Section 4 explains the architecture of SCOR, and Section 5 and Section 6 describe its implementation and use cases. Section 7 discusses the evaluation methodology and results and Section 8 concludes the paper.

2. Background: Constraint Programming

Constraint-Programming (CP) techniques were initially introduced in the 1960s and 1970s in artificial intelligence and computer graphics. They have found applications in many fields such as operations research, programming languages and databases (Rossi et al. 2006). The main idea behind CP is to separate the expression of a problem from its solution. Users are only required to state the problem and the solution is found by general-purpose constraint solvers which are designed for this purpose.

This allows for very flexible modelling of problems and their efficient solution, for large, particularly combinatorial problems (Bartak 1999). In order to use CP to solve a real world problem, it must be stated in the form of a CP model. A CP model includes at least three parts:

• Decision variables that represent tasks, metrics or resources of a real world problem.
• Variable domains that are a finite set of possible values for each decision variable.
• Constraints that state the relations (conditions, limitations, properties and bounds) between decision variables.

The constraints in fact restrict the values that all decision variables can have for a particular solution (Bartak 1999). The solution of a CP model is the allocation of values to the decision variables from their domains that simultaneously satisfy all the constraints. Accordingly, CP problems are called Constraint Satisfaction Problems (CSP). The solver can provide a single solution, the first one that satisfies the constraints, all possible solutions, or the one that maximises or minimises a provided objective function.

If an objective function is defined, the problem is called a Constrained Optimisation Problem (OP) (Bartak 1999). The solvers enumerate possible variable-value combinations intelligently and search the solution space either systematically or through some forms of complete or incomplete search methods. The performance of these methods depends on the nature and statement of the problem (Rossi et al. 2006).

3. Related Works

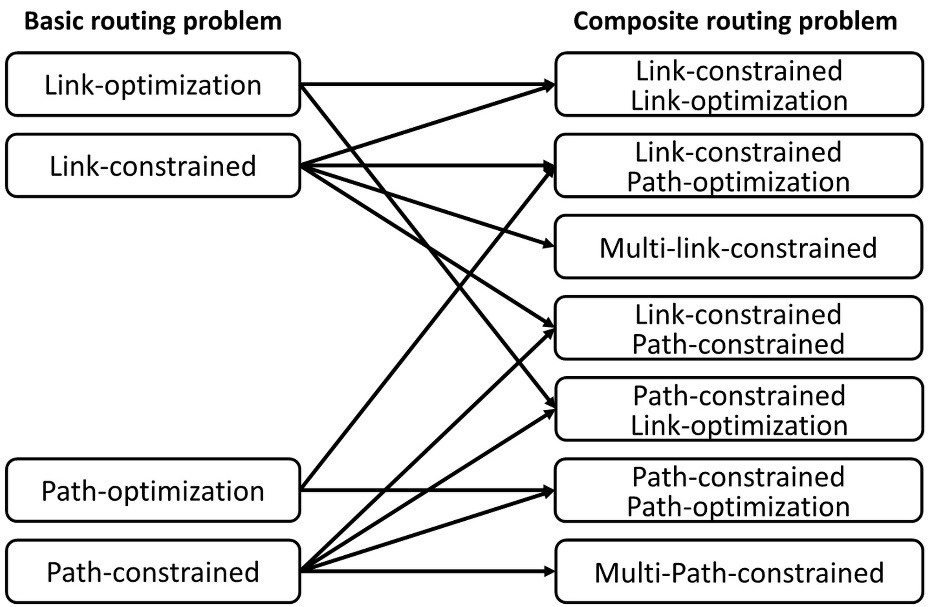
Different types of classifications are proposed for QoS routing in legacy networks. The classification shown in Fig. 1 is proposed by Chen & Nahrstedt (1998). It divides the unicast routing problems into two major categories: basic and composite routing problems. The criterion used for this classification is the number of QoS metrics applied in the problem. A basic routing problem includes only a single QoS metric such as delay, jitter or bandwidth. The routing problem in this case might consist of metric optimisation, such as finding a minimum delay path, or it might include metric constraining, such as finding a bandwidth-constrained path. In addition, the metric might be related to a link parameter, e.g. bandwidth, or it might be related to a path parameter, such as end-to-end delay. The composite routing problems represent multi-constraint QoS routing problems. They can be expressed as the combination of a single-metric-optimisation problem with one or more metric-constraining problems, or just the combination of two or more metric-constraining problems.

Figure 1 : Basic and composite QoS routing problems (Chen & Nahrstedt 1998)

In SDN though, limited work has been done on QoS routing problems. Indeed, there is currently no northbound interface that provides the required abstractions for implementing all the above basic and composite QoS routing algorithms. While there exist a number of controller-proprietary northbound interfaces, they tend to deal with packet and port-level manipulations rather than higher-level routing and QoS routing abstractions. The PANE controller (Ferguson et al. 2013) and SFNet northbound interface (Yap et al. 2010) are two examples of implementing QoS abstractions in SDN. However, their limited functionality and scope restricts the range of QoS routing applications that can be implemented.

DEFO (Hartert et al. 2015) is a recent approach to control forwarding paths in non-SDN carrier grade networks. It uses CP for network optimisation and to efficiently address QoS routing requirements. Using CP and new heuristics has enabled DEFO to achieve a significant increase in scalability and flexibility in traditional networks. While DEFO includes features for expressing QoS routing and TE requirements using CP, it has not been designed for SDNs, and does not provide a suitable northbound interface. In this paper, we are trying to address this gap, by providing a new northbound interface in SDN that facilitates development of QoS routing and traffic engineering applications in an efficient and scalable way.

4. Architecture

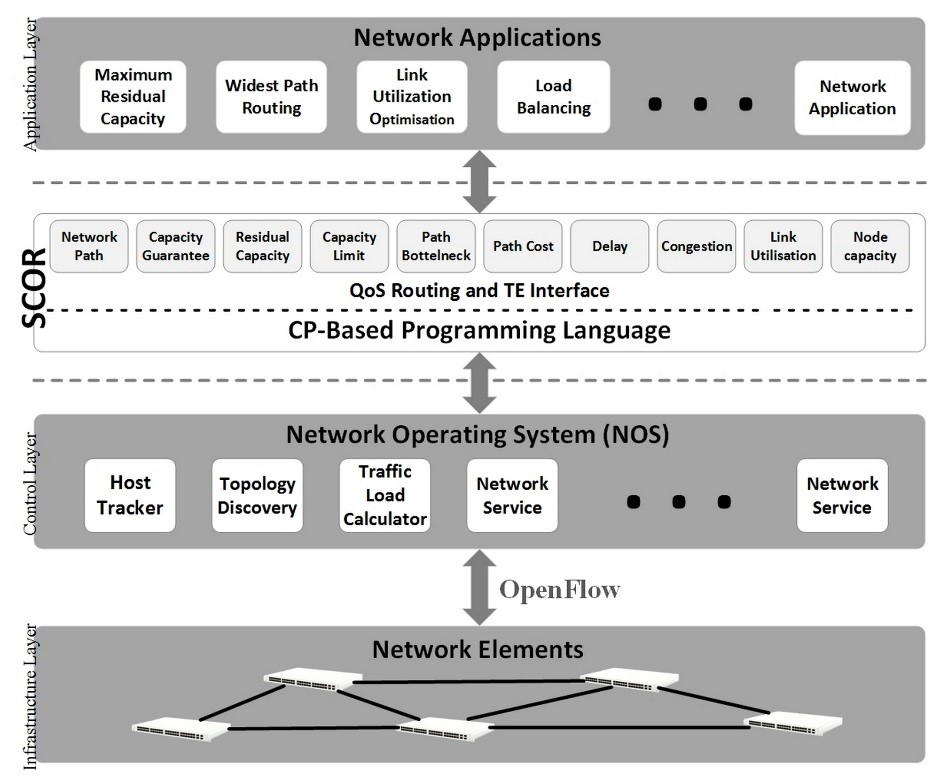
Fig. 2 shows the integration of SCOR in the SDN architecture, between the application and control layer. SCOR consists of two layers which represent two levels of programming abstractions. The bottom level is the generic CP-based Programming Language and the higher level is the set of predicates which form the QoS Routing and TE Interface. The second layer, the QoS routing and TE interface, is specifically designed to address QoS routing and TE requirements. It consists of 10 building blocks or predicates, as listed in Table 1.

Figure 2 : Situation of SCOR in the SDN architecture

The most basic concept in routing that we need to model in SCOR is that of a network path, i.e. a sequence of links which connect two nodes. The network path predicate defines a loop-free path from a flow source to its destination. The rest of the predicates implement other constraints which are required in QoS routing applications such as capacity constraint and cost. These are the required building blocks for modelling both basic and composite routing problems as seen in Fig. 1.

The capacity guarantee predicate implements the capacity constraint, which guarantees flows are placed only on links that can accommodate them. Whenever flow demands are considered in a QoS routing application, knowing the available capacity in the network is necessary for accommodating them. The residual capacity predicate is created to provide these values by defining the residual capacity of all links, assuming all the known flow demands are routed. The capacity limit predicate removes links with a capacity less than a specified limit from the path calculation. The path bottleneck predicate defines the bottleneck capacity for a given path, which is required when considering the bandwidth optimisation problem in QoS routing. The path cost, a frequently utilised networking concept, is modelled by the path cost predicate. It is possible to assign various parameters for the cost, such as loss, delay, round trip time (RTT), number of hops, etc.

Table 1: Set of predicates forming QoS routing and TE interface of SCOR

There are TE problems in which the desired network parameters dynamically change with the traffic. For instance, the queueing delay in each network node not only depends on the capacity of network paths, but it also depends on the amount of traffic flowing into the network. These TE applications which are mostly defined based on the residual capacity concept are covered by the delay, congestion and link utilisation predicates.

The last predicate, node capacity, is designed to model the half-duplex transmission nature of many wireless networks, as well as other shared media access networks. In the half-duplex transmission mode, a node can either send or receive data, but not both simultaneously. This can be stated as "the capacity of a half-duplex node to send the traffic is reduced by the amount of traffic it is currently receiving". It is possible to implement this concept or constraint in a range of ways, we have implemented it via imposing a total capacity constraint per node (i.e. network interface card), considering both ingress and egress traffic. This constraint is imposed in addition to other constraints, in particular the link capacity constraint.

5. Implementation

SCOR is implemented in MiniZinc (Nethercote et al. 2007) which is a declarative CP modelling language. It comes with a set of pre-packaged solvers, but it can easily use other solvers as well. The ease of implementation, simplicity, expressiveness and compatibility with many solvers has made it a good choice for the basis of SCOR. MiniZinc includes a rich library of global constraints which model high-level CP abstractions (Nethercote et al. 2007). A problem is stated in MiniZinc in two parts, the model and model data. The model uses parameters, decision variables and constraints to describe the structure of a CP problem. The model data includes the values of static parameters that are determined when the problem is defined, e.g. in a separate file. The values of decision variables are undecided and they are determined by the solver. Different model data can be used with a single model to designate various problem scenarios (Nethercote et al. 2014). MiniZinc includes predicates that are similar to functions or methods in procedural programming languages for creating abstractions, modularity and code reuse. Predicates define higher-level constraints and can be included in a model using an include item (e.g.  include "globals.mzn";). MiniZinc expressions, syntax and a wide range of examples are explained in detail in the MiniZinc tutorial (Marriott et al. 2014).

Using the above-mentioned MiniZinc concepts, we can define the network path predicate, which plays a fundamental role in SCOR. The network path predicate uses the flow conservation concept to define a flow path. The flow conservation rule is explained as follows. We assume a directed graph representing a network topology.

The set of network nodes is represented by  and represents the graph arcs i.e. network links. Links are assumed multi-weighted with the weights being scalars representing various link parameters such as capacity, delay and cost. The flow of a link defines the quantity of units, e.g. expressed in Kbps or Mbps, which flows between a source  and a destination . Given the directed nature of ,  is not necessarily the same as . With this, the flow conservation rule can be stated as follows:

                                               (1)

Eq. 1states that for a unit flow, except for the source  and destination , the sum of the flows arriving at each node is equal to sum of the flows leaving it. This constraint defines a network path, i.e. a contiguous list of links connecting a source and a destination node.

The MiniZinc code that defines the flow conservation rule and hence implements the network path predicate, is shown in Predicate 1. In this code  and  represent the number of nodes and links respectively, and  and  are the source and destination nodes of the flow.  is a 2-dimensional array, with each row representing a link. In our implementation, a row (or link)  consists of the following four elements , with  and  representing the source and destination node, and  and  representing 2 link weights. The choice of 2 for the number of link weights is arbitrary, and can easily be extended to any required number. , the Link Path Membership, is an array of binary decision variables, which indicate which links belong to a path.  means that link  belongs to a path, and  means that it does not.

In lines 2-4 of Predicate 1, the flow conservation rule is applied to all nodes. Line 2 defines the total flow arriving at node . This is done by summing up the link-path-memberships of the links in which node  is the destination node, i.e. . (The Boolean operator  represents conjunction, i.e. logical AND.) Line 3 defines the total flow leaving node  in a similar manner. Line 4 applies the equality constraint of the flow arriving and departing each node, with the exception of the source and destination nodes.

The definition of a path via the flow conservation rule expressed in lines 1-4 does not prohibit routing loops. The additional constraint in line 5, which says that a flow can arrive at a node at most once, guarantees paths are loop free. For simplicity, we have discussed the network path predicate for a single flow only. However, our implementation supports any number of flows.

Due to lack of space, we only discuss the core predicates here. The complete details of all SCOR predicates and their implementation are available in (Layeghy et al. 2016).

6. Use cases: QoS Routing Applications

6.1 Least Cost Path Routing

In this section, we explain how we implemented basic least cost path routing using SCOR. We use our previously described representation of a network as a graph  with multi-weighted links. In least cost path routing, the problem is to find a path with the minimum total cost between a source node  and destination node   (Bertsekas 1998). This can be stated as the following optimisation problem:

where flow  is stated as the multiplication of its demand, , and , a binary variable indicating of whether the link  is a part of the flow path. The parameter  is the weight of link  which represents the link cost. In practice, these cost values can be used to represent various link parameters such as delay, lease price, packet loss ratio, etc. This makes it possible to model the corresponding QoS routing algorithms in SCOR.

The solution of the problem can be stated as a sequence of links that connects the flow source to the flow destination and has the minimum sum of link costs. Several algorithms such as Dijkstra and Bellman-Ford can efficiently solve this problem in procedural programming (Mir 2014). In SCOR though, the implementation only includes the declaration of the problem, and not how to solve it, as it can be seen in Model 1. Lines 1 and 2 are include items which make it possible to use two predicates, network path and path cost. Lines 3-7 declare the parameters which are required to model the least cost path problem. The  array/matrix not only states the links start and end nodes, but it also states the corresponding values of link cost and capacity. Lines 8-9 also declare the two decision variables,  and . The first variable, , represents the  as declared in Eq. 4 and  is the total cost of the flow path.

The main body of the program includes the Constraints item (lines 10-11) and the Solve item (line 12). The first constraint, network path predicate, defines the path from the flow source node  to its destination node . The second constraint, path cost predicate, defines the cost associated with the path. The solve item indicates the objective, i.e. what the solver should optimise, which is the path cost.

6.2 Least Cost Path Routing with Capacity Constraint

Using SCOR predicates as building blocks, it is easy to state a wide range of QoS routing problems. Here we explain how a new routing application can be defined by adding SCOR predicates to the previously implemented models. For instance, the least cost path routing with capacity/bandwidth constraint problem can be modelled by simply adding a new predicate to the least cost path routing model. In this problem, we are looking for the least cost path that provides a minimum end-to-end capacity of . This least cost path routing with capacity constraint problem can be formally stated as the following optimisation problem:

 where  is the bandwidth/capacity constraint applied to the flow and other parameters are similar to those of the previous model. This is essentially the same as the least cost path routing problem, with the only addition of an additional constraint (8).

Our implementation of this problem is shown in Model 2 which only includes the lines of code added to Model 1. It shows that only three additional lines of code are required to turn the least cost path routing model into the least cost path routing with capacity constraints model. The first added line (line 1) is an include item which calls the capacity limit predicate. The next added line of code (line 2) defines a new parameter, , which states the associated bandwidth/capacity limit or bound. Finally, the last added line (line 3) is the new capacity constraint.

6.3 Maximum Residual Capacity Routing

The third routing application modelled in SCOR is the Maximum Residual Capacity (MRC) routing. Unlike two previous models, this application addresses the problem of routing multiple concurrent flows in a network. The main objective here is to route flows in a network, so that the minimum residual link capacity is maximised. The residual (or available) capacity of a link is the difference between its capacity and the total flow passing through it. Sending a traffic flow in a way that the minimum available capacity of the network is maximised, increases the chance of having sufficient capacity to accommodate the next flow request (Walkowiak 2006).

This is a complex optimisation problem which is also known as the Non-Bifurcated Congestion (NBC) problem,  in the context of multi-commodity flow problems. For a set of concurrent flows to be routed through  where source of flow  is  and its destination is , the problem can be stated as the following optimisation problem (Walkowiak 2006):

 The objective is to maximise  (Eq. 9), where it is less than or equal to the residual capacity of all links  (Eq. 10), subject to the capacity and flow conservation constraints. The residual capacity of the links, , is given by (Eq. 11). The capacity constraint (Eq. 12) states the total flow of a link, , should be less than or equal to the link's capacity, The total flow of a link, , is sum of all individual flows on the link,  (Eq. 13). Finally, Eq. 14 is the flow conservation rule for a single flow  with a demand of . In order to implement the flow conservation for individual flows with non-unitary demands, flows are stated as:

where  is equivalent to the previously mentioned link-path-membership variable.

A wide range of heuristic solutions for the above problem have been presented in the context of procedural programming, which typically are complex and require many lines of code for the implementation. In contrast, the implementation in SCOR, shown in Model 3, is as simple as the least cost path routing model. The key difference is contained to lines 13 and 14, which implement the residual capacity constraint and state the optimisation objective. Similar to Model 1, lines 1-2 are include items which call two predicates, network path and capacity guarantee. Lines 3-9 define the parameters such as , , etc. Line 10-11 declare the two decision variables,  and , that define link-path-membership and the residual capacity of links respectively. Line 12 implements the network path constraint and line 13 implements the capacity guarantee constraint which defines the residual capacity and constrains them to be greater than or equal to zero (implementing Eq. 11 and Eq. 12). Finally, line 14 states the objective function, which aims to maximise the minimum of  (implementing Eq. 9 and Eq. 10).

6.3 Wireless Maximum Residual Capacity Routing

The Wireless Maximum Residual Capacity (WMRC) model aims to extend the previous model, by considering the half-duplex nature of many wireless networks nodes. In half-duplex networks, a node can either send or receive, but not both at the same time. This essentially limits the capacity of the node. We have modelled this constraint in the new node capacity predicate in SCOR, and we will demonstrate its use for residual capacity routing in wireless (half-duplex) networks.

The mathematical formulation of the problem is similar to previous problem, maximum residual capacity routing, with the addition of the following additional constraint:

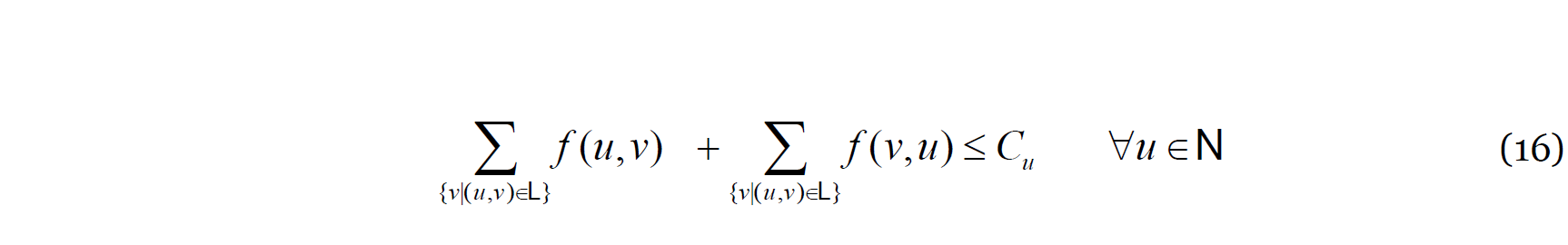Here,  is the node  capacity/limit that indicates the total traffic flow that a node can handle. This equation constraints the total flows entering and leaving a node to be equal or less than . As mentioned, this extra constraint is implemented in the node capacity predicate and is added to Model 3. The implementation of WMRC is shown in Model 4. The first added line (line 1) calls the node capacity predicate, the second line (line 2) declares a new parameter, , which defines the acceptable amount of flows for each node, and line 3 applies the above constraint (Eq. 16).

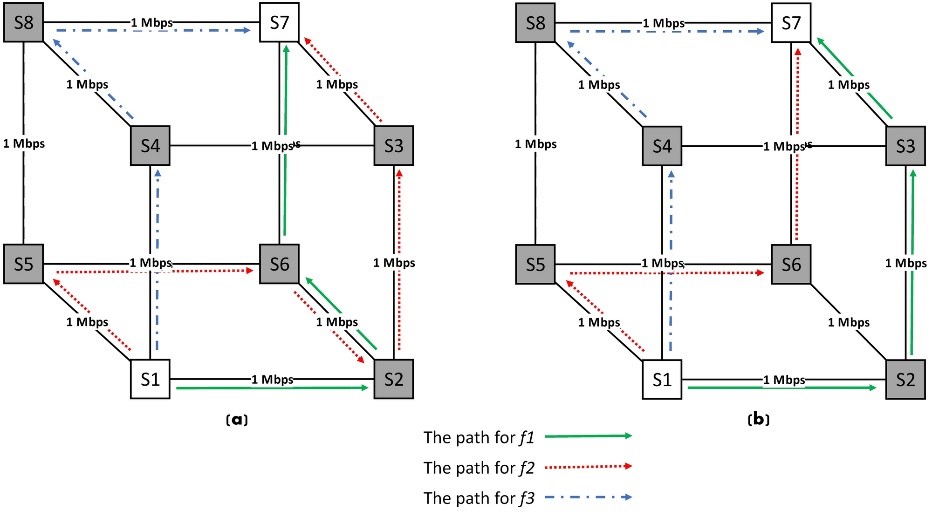
In order to illustrate how adding the new constraint affects the paths found by the model and consequently the network performance, we use the below scenario. In the network topology shown in Fig. 3, there are three concurrent flows with equal demand of 1 Mbps to be routed from node S1 to node S7. All links are bidirectional with an equal capacity of 1 Mbps in each direction (bidirectional links are mathematically represented using two unidirectional links). (To illustrate the concept, we assume nodes S1 and S7  have no node capacity limitations, e.g. they are equipped with faster or multiple network interfaces. ) Shortest path routing, which uses only one of the three equivalent shortest paths from node  to node , theoretically can send 1 Mbps as shown in Fig. 4.

For this scenario, the MRC model finds the three paths as the following sequence of links (shown in Fig. 3-a):

• f1: {(S1,S2),(S2,S6),(S6,S7)}
• f2: {(S1,S5),(S5,S6),(S6,S2),(S2,S3),(S3,S7)}
• f3: {(S1,S4),(S4,S8),(S8,S7)}

The path f2 is not the shortest possible path from node  to node , though, it is a valid path according to the criteria for the maximum residual capacity routing. Although links  and  are both connecting node  and , they are considered separate links in full duplex transmission. So the three concurrent flows of 1 Mbps are successfully transmitted to the destination node.

Figure 3: Paths found for three concurrent flows from node 1 to node 7 using a) Maximum residual capacity model (MRC), and b) Wireless maximum residual capacity model (WMRC)

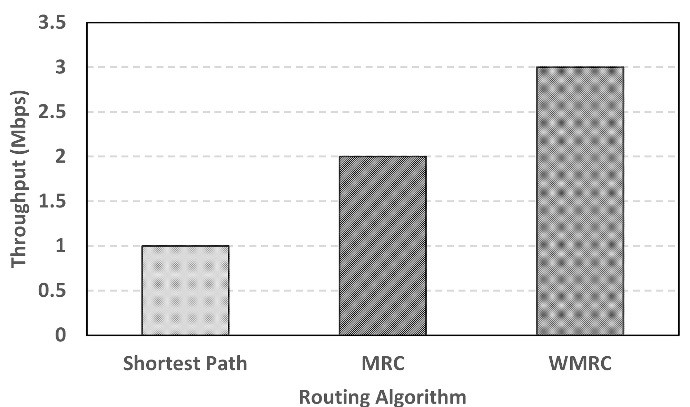
However, in networks which use half-duplex transmission,  the situation is different. For these networks, the traffic received by a node limits the amount of traffic that can be simultaneously sent by that node. In this case, the theoretical throughput from node  to node , using the three paths found by the MRC model, is only about 2 Mbps, as shown in Fig. 4. The reason for the limited performance in this case is node S6, which needs to receive and transmist two flows simultaneously, and hence is the bottleneck.

Figure 4: Theoretical throughput for three concurrent flows of 1 Mbps in a half duplex network with a topology as shown in Fig. 3 (node  is the source and node  is destination) in the case of Shortest path routing, MRC and WMRC models

Now we use Model 4, WMRC, to find the paths.  Since it considers the half-duplex nature of links, modelled as a node capacity limit of 1 Mbps, the WMRC model finds the following three flow paths (shown in Fig. 3-b):

• f1: {(S1,S2),(S2,S3),(S3,S7)}
• f2: {(S1,S5),(S5,S6),(S6,S7)}
• f3: {(S1,S4),(S4,S8),(S8,S7)}

As in the previous case, all links have a capacity of 1 Mbps, and we impose a node capacity limit of 1 Mbps for each node except source and destination, i.e. S1 and S7. As a result of the half-duplex constraint in the WMRC, the impact of node bottlenecks can be minimised, and the aggregate throughput achieved by the above shown 3 paths is 3 Mbps, instead of 2 Mbps of MRC. 

This example tries to show how easy it is to add/model new network constraints and features in SCOR, and consequently how easy it is to implement complex QoS routing problems. Our WMRC example is very simple and it only addresses one particular aspect of typical wireless networks, i.e. the half-duplex nature of transmission.  The modularity and extendebility of SCOR allows us to easily add further predicates and building blocks, which can model more complex aspects of wireless networks, such as interference.

7. Evaluation

The evaluation of SCOR includes two aspects, the first one being the completeness of the API, i.e. the set of predicates, and its ability to concisely express a wide range of QoS routing problems. The second aspect is the efficiency and scalability of finding valid solutions. The completeness aspect of SCOR was briefly discussed in Section 4. SCOR's set of predicates support the modelling of all QoS routing problems, as classified in Fig. 1. Table 2 shows a list of basic and composite QoS routing problems which we were able to model and solve with SCOR. The table shows the SCOR predicates that were used for each problem, as well as the number of lines of SCOR/MiniZinc code (excluding boilerplate code) that were required for the problem formulation. The network path predicate is used in all of these problems and models, and in order to save space, we did not include it in the table.

Table 2: QoS routing algorithms and predicates to model them in SCOR

Table 2 clearly shows the expressiveness of SCOR and its power to model complex QoS routing problems. Furthermore, we see that the formulation in SCOR is extremely compact, with a maximum of 4 lines of SCOR/MiniZinc code. This is due SCOR's high level of abstraction.

The second, equally important aspect in the evaluation of SCOR is its scalability and ability to quickly and efficiently find valid solutions to the routing problems. For this, we examined the solve-time of the three implemented QoS routing problems for two network topologies and a range of network sizes. We considered grid and fat-tree topologies in our experiments. The fat-tree topology we used is defined in (Al-Fares et al. 2008). It is parametrised by , and consists of three layers, with  nodes in the core layer,  nodes in the aggregation layer, and  nodes in the access layer. Each access node (switch) is connected to  hosts.

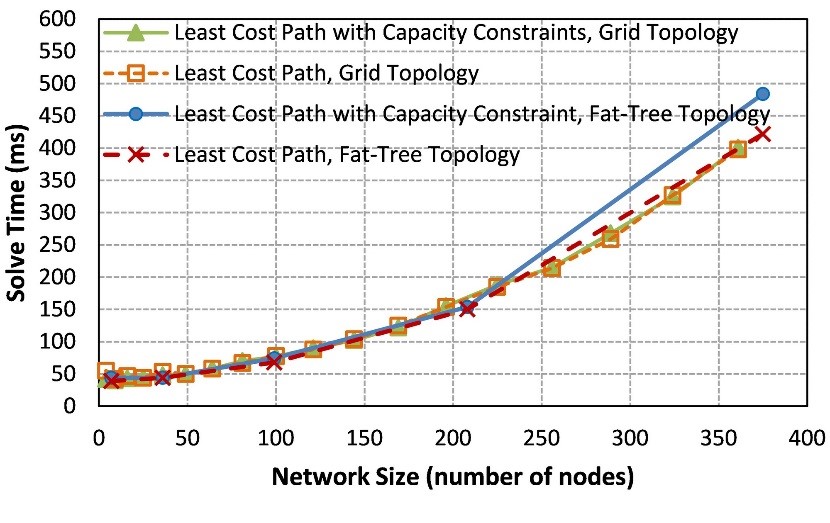
Fig. 5 displays the solve-time for the Least Cost Path and Least Cost Path with Capacity Constraint routing problems with SCOR. For our experiments, we used MiniZinc's default solver. All experiments were run on a Dell PC with Intel Core i7-4790 CPU and 16 GB of RAM, running Linux with the kernel version of 3.13.0-24-generic. The x-axis shows the network size, and the y-axis shows the solve-time in milliseconds. As can be seen, for both routing problems, the solve time remains below 500 ms, even for relatively large network sizes of greater than 350 nodes. This demonstrates the practical feasibility of using SCOR/MiniZinc to solve complex routing problems in near real time.

Figure 5: Solve time for the Least Cost Path and Least Cost Path with Capacity Constraint problem in fat-tree and grid topologies with various network sizes

A key benefit of SCOR is that it shields the user from the complexity of solving hard optimisation problems. SCOR leverages the power of highly sophisticated constrained optimisation solvers, such as those provided with MiniZinc. The advantage of our approach is particularly significant for QoS routing problems for which no efficient solution/algorithm exists, and which rely on heuristics. An example is the maximum residual capacity routing problem (Walkowiak 2006).

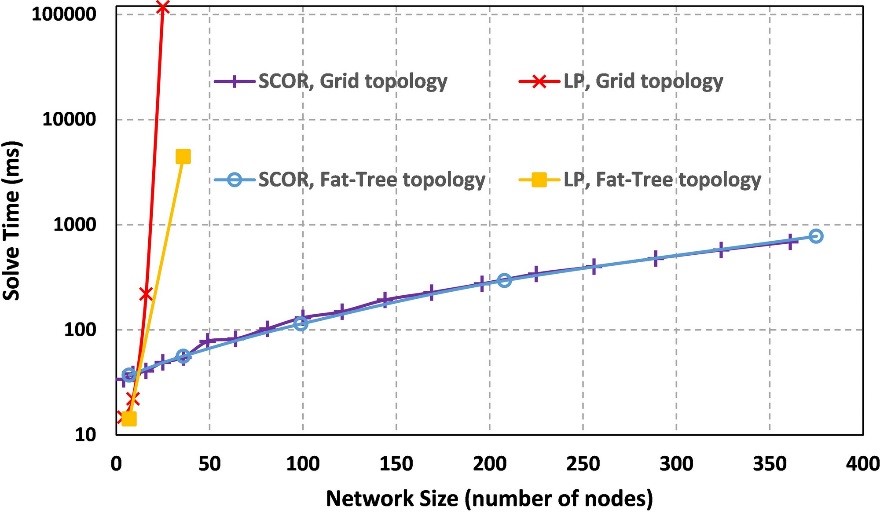
Fig. 6 compares the solve-time for the maximum residual capacity routing problem in SCOR, with an algorithm using a linear programming (LP) approach, presented in Walkowiak (2006). The LP solution is implemented in Python using the NetworkX and PuLP (Mitchell et al. 2011) libraries. We used the same regular grid and fat-tree topologies of varying sizes as in our previous experiment. As before, the x-axis shows the network size, and the y-axis shows the solve-time in ms. Due to the multiple order of magnitude better performance of SCOR/MiniZinc, we used a logarithmic scale for the y-axis. The LP algorithm was not able to find a solution for a network size of 50 nodes or more, even in a time of 24 hours. In contrast, SCOR/MiniZinc was able to find solutions in under a second, even for networks with more than 350 nodes.

Figure 6: The solution time for the Maximum Residual Capacity problem compared to LP in fat-tree and grid topologies with various network sizes

Hence, SCOR is able to solve complex optimisation problems, such as maximum residual capacity routing,  with a speed that is at least as fast as comparable prodecurable programming solutions. The benefit of SCOR lies in the power of its abstraction, its modularity, and simplicity in which complex QoS routing problems can be expressed and solved. 

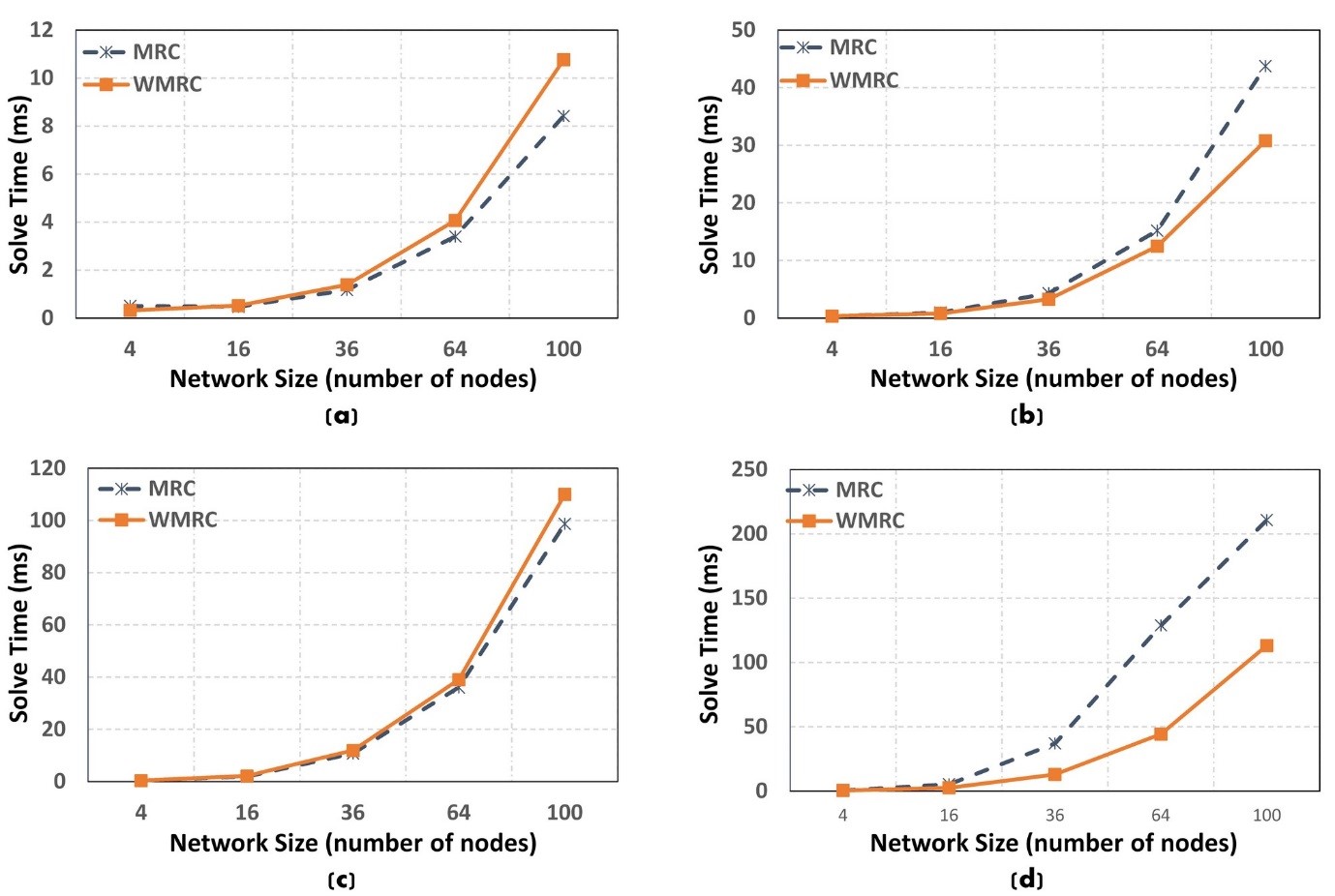
Fig. 7 shows the comparison of solve times of the MRC and WMRC model. The figure compares the solve times for different network sizes and various numbers of concurrent flows in each sub-figures. Fig. 7a compares the solve times for routing a single flow, Fig. 7b two concurrent flows, Fig. 7c three concurrent flows, and finally Fig. 7d compares the solve time for routing four concurrent flows. These results indicate that the added constraint does not increase the solve time significantly, it even reduces the solve time for the WMRC model compared to MRC in some cases (Fig. 7a and 7c).

Figure 7: The solution time for the Maximum Residual Capacity (MRC) model and Wireless Maximum Residual Capacity (WMRC) model in grid topologies with various network sizes in the case a) One flow, b) Two concurrent flows, c) Three concurrent flows, and d) Four concurrent flows

Similar results regarding the power of CP solvers, supporting our findings, were also reported in (Hartert et al. 2015). The authors considered the use of CP programming to solve routing problems in traditional, non-SDN networks, and reported a multiple order of magnitude faster solve-time of the CP solver compared to an LP approach. In summary, SCOR's expressiveness and solving efficiency of complex QoS routing problems has shown very promising results in both aspects. We have implemented SCOR as a component on the POX SDN controller platform. More details on the implementation are available in our technical report (Layeghy et al. 2016).

8. Conclusion

The main contribution of this work is the introduction of a new northbound interface for SDN, based on constraint-programming techniques. The fundamental goal in the design of this northbound interface is to reduce the complexity of implementing QoS routing and TE applications in SDN, by providing an appropriate level of abstraction. SCOR, the proposed solution, provides the necessary building blocks, i.e. the predicates, to express complex routing problems in a very compact and simple manner, as we have demonstrated. A key aspect is the ease in which predicates can be combined, nested and reused.

A powerful aspect of SCOR, which it inherits from constraint programming, is the separation of the problem formulation and its solution. SCOR's layer of abstraction hides the complexity of the problem solution from the user, and therefore greatly simplifies the implementation of new routing and traffic engineering applications. The increased level of abstraction and simplicity does not at all come at a cost of reduced efficiency. Through the use of powerful generic constraint programming solvers, solutions to complex QoS routing problems can be found faster than through traditional procedural programming solutions, in some cases by orders of magnitude, as we have shown.

While we have focused on the application of SCOR for QoS routing and traffic engineering, we believe it has wider applicability, e.g. in security. We can envisage that security policies can be expressed as constraints in SCOR, and the guaranteed enforcement is delegated to the solver.

As mentioned, SCOR is currently implemented as a component in the POX controller. We are currently working on an implementation of SCOR in ONOS  (Berde et al. 2014). We believe that SCOR adds a powerful and practical layer of abstraction to SDN, which greatly simplifies the problem of QoS routing, traffic engineering and possibly a range of other network applications.

References

Al-Fares, M.; Loukissas, A.; Vahdat, A. (2008). A scalable, commodity data center network architecture. Paper presented at the Proceedings of the ACM SIGCOMM 2008 conference on Data communication, Seattle, WA, USA.

Bartak, R. (1999). Constraint Programming: In Pursuit of the Holy Grail. Paper presented at the In Proceedings of the Week of Doctoral Students (WDS99 -invited lecture).

Berde, P.; Gerola, M.; Hart, J.; Higuchi, Y.; Kobayashi, M.; Koide, T.; Lantz, B.; O'Connor, B.; Radoslavov, P.; Snow, W.; Parulkar, G. (2014). ONOS: towards an open, distributed SDN OS. Paper presented at the Proceedings of the third workshop on Hot topics in software defined networking, Chicago, Illinois, USA.

Bertsekas, D. P. (1998). Network optimization: continuous and discrete models. Belmont Massachusetts, USA: Athena Scientific.

Chen, S.; Nahrstedt, K. (1998). An overview of quality-of-service routing for next-generation high-speed networks: problems and solutions. Network, IEEE, 12(6), 64-79. doi:10.1109/65.752646

Curado, M.; Monteiro, E. (2004). A survey of QoS routing algorithms. Paper presented at the International Conference on Information Technology (ICIT 2004), Istanbul, Turkey.

Ferguson, A. D.; Guha, A.; Liang, C.; Fonseca, R.; Krishnamurthi, S. (2013). Participatory networking: an API for application control of SDNs. SIGCOMM Comput. Commun. Rev., 43(4), 327-338. doi:10.1145/2534169.2486003

Gallager, R. G. (1977). A Minimum Delay Routing Algorithm Using Distributed Computation. IEEE Transactions on Communications, 25(1), 73-85. doi:10.1109/TCOM.1977.1093711

Hartert, R.; Filsfils, C.; Vissicchio, S.; Telkamp, T.; Schaus, P.; Francois, P.; Bonaventure, O. (2015). A Declarative and Expressive Approach to Control Forwarding Paths in Carrier-Grade Networks. Paper presented at the ACM Conference on Special Interest Group on Data Communication - SIGCOMM '15, New York.

Kreutz, D.; Ramos, F. M. V.; Verissimo, P. E.; Rothenberg, C. E.; Azodolmolky, S.; Uhlig, S. (2015). Software-Defined Networking: A Comprehensive Survey. Proceedings of the IEEE, 103(1), 14-76. doi:10.1109/JPROC.2014.2371999

Layeghy, S.; Pakzad, F.; Portmann, M. (2016). SCOR: Software-defined Constrained Optimal Routing Platform for SDN. arXiv preprint arXiv:1607.03243.

Ma, Q.; Steenkiste, P. (1997). Quality-of-Service Routing for Traffic with Performance Guarantees. In A. Campbell & K. Nahrstedt (Eds.), Building QoS into Distributed Systems (pp. 115-126): Springer US.

Marriott, K.; Stuckey, P. J.; Koninck, L. D.; Samulowitz, H. (2014). A MiniZinc Tutorial.   Retrieved from https://www.minizinc.org/downloads/doc-latest/minizinc-tute.pdf

McKeown, N. (2009). Software-defined networking. INFOCOM keynote talk, 17(2), 30-32.

Mir, N. (2014). Computer and Communication Networks, 2nd Edition (Vol. 1). London: Prentice Hall.

Mitchell, S.; OSullivan, M.; Dunning, I. (2011). PuLP: a linear programming toolkit for python. The University of Auckland, Auckland, New Zealand, http://www. optimization-online. org/DB_FILE/2011/09/3178. pdf.

Moreira Jr, W. A. M.; Aguiar, E.; Abel?m, A.; Stanton, M. (2008). Using multiple metrics with the optimized link state routing protocol for wireless mesh networks. Simp?Usio Brasileiro de Redes de Computadores e Sistemas DistribuIdos.

Nethercote, N.; Marriott, K.; Rafeh, R.; Wallace, M.; Banda, M. ?. G. ?. d. l. (2014). Specification of MiniZinc. In NICTA (Ed.). Victoria Research Lab, Melbourne, Australia: NICTA.

Nethercote, N.; Stuckey, P. J.; Becket, R.; Brand, S.; Duck, G. J.; Tack, G. (2007). MiniZinc: Towards a Standard CP Modelling Language. In C. Bessi?re (Ed.), Principles and Practice of Constraint Programming ? CP 2007 (Vol. 4741, pp. 529-543): Springer Berlin Heidelberg.

Patel, M.; Chandrasekaran, R.; Venkatesan, S. (2004). Efficient Minimum-Cost Bandwidth-Constrained Routing in Wireless Sensor Networks. Paper presented at the International Conference on Wireless Networks.

Rossi, F.; Beek, P. V.; Walsh, T. (Eds.). (2006). Handbook of constraint programming (Vol. 1). UK: Elsevier.

Walkowiak, K. (2006). Maximizing residual capacity in connection-oriented networks. Journal of Applied Mathematics and Decision Sciences, 2006, 18. doi:10.1155/jamds/2006/72547

Yap, K.-K.; Huang, T.-Y.; Dodson, B.; Lam, M. S.; McKeown, N. (2010). Towards software-friendly networks. Paper presented at the Proceedings of the first ACM asia-pacific workshop on Workshop on systems, New Delhi, India.