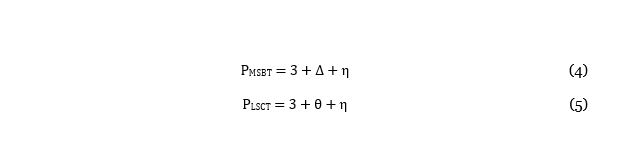1. Introduction

The Residential Gateway Router (RGR) has traditionally been used to connect the Local Area Network (LAN) in the home with the Wide Area Network (WAN) of the service providers. Services such as Internet Protocol Television (IPTV), media sharing, home security and other value added services are driving the RGR from its traditional function of simple packet forwarding applications. The home network has gained prominence in the networking ecosystem due to the emergence of the smart home and an increased presence of consumer Internet of Things (IoT) devices in the home network. Moreover, researchers have found various security vulnerabilities in the RGR and have identified that it is easy prey for network attacks (Holcomb, 2016; Team Cymru Threat Intelligence Group, 2016). Value added services, such as content-based Quality of Service (QoS), and security applications, such as intrusion prevention, drive the need for Content Aware Networking (CAN) in the home network. Moreover, improving broadband speeds (Sappington, 2016) necessitate the need for multi-gigabit line-rate packet processing, not only for packet forwarding applications in the RGR but also for content aware networking applications.

Deep Packet Inspection (DPI) is the process of inspecting the network packet payloads with a predefined database of signatures to perform CAN. DPI has various functions, which include network packet normalization (Handley, Paxson & Kreibich, 2001), flow based packet reordering, signature subset allocation based on header analysis (Song et al., 2005), signature matching and packet post processing (Xu, 2016). However, signature matching is the most time critical function in DPI and defines the rate at which DPI can be performed in modern network processors (Nourani & Katta, 2007). Considering the processing and memory capabilities of the RGR, an analysis in Subramanian, Lin & Herkersdorf (2014) identified that hardware acceleration of signature matching is essential to support line-rate DPI in the RGR.

The signatures which are used for DPI applications comprise strings and regular expressions and are used to identify the patterns in the network traffic. Since automata-based methodologies support both string and regular expression signatures, the signature set is converted into an automaton (state table) with which the network payload is compared (Becchi & Crowley, 2007). The signatures can either be converted into a Non-Deterministic Finite Automaton (NFA) or a Deterministic Finite Automaton (DFA) to perform the signature matching against the network traffic. The NFA is time inefficient and space efficient, while the DFA is time efficient and space inefficient (Yu et al., 2006). DFA-based architectures are preferred over NFA-based architectures, as they allow the signature matching to be done in linear time (Becchi & Crowley, 2007). A set of signatures can be converted into a DFA based on the algorithms described in John, Rajeev & Ullman (2007).

The DFA represents the signatures in the form of a finite state machine with states and directed edges between the states to represent the state transitions (Xu, 2016). Since the internet traffic is primarily constructed over the extended ASCII character set, each state in the DFA has 256 outgoing transitions, while the total number of states in the DFA depends on the characteristics of the signatures which it represents (Becchi & Crowley, 2007b). Various compression algorithms have been proposed in the literature to address the storage inefficiency associated with the DFA and can be further classified into transition and state compression algorithms (Xu, 2016). The transition compression algorithms focus on compressing the redundant state transitions in the DFA, while the state compression algorithms focus on reducing the number of states in the DFA. However, the transition and the state compression algorithms are orthogonal to each other (Xu, 2016).

Certain regular expressions contain terms such as the Kleene closure operator which, when it interacts with other signatures, results in an exponential growth in the number of states generated in the DFA. This is referred to as the state explosion problem (Becchi & Crowley, 2007b). Many modified automata such as the Hybrid Finite Automaton (HFA) (Becchi & Crowley, 2007b), eXtended Finite Automaton (XFA) (Smith et al., 2008), Tunable Finite Automaton (TFA) (Yang et al., 2014), Jump Finite Automaton (JFA) (Yu, Lin & Becchi, 2014) and DFA with Extended Character Set (DFA/EC) (Cong et al., 2014) have been proposed in the literature to counter the state explosion problem.

The transition compression algorithms proposed in the literature can be classified into hardware-oriented and software-oriented algorithms (Subramanian et al., 2016). The software oriented transition compression techniques such as the D²FA (Kumar et al., 2006), A-DFA (Becchi & Crowley, 2013), δFA (Ficara et al., 2008) and RCDFA (Rafael et al., 2015) compress the redundant state transitions in the DFA at the cost of additional memory bandwidth to fetch the compressed state transition (Xu, 2016). Moreover, multiple terabits of on-chip memory bandwidth will be required, when the signature matching has to be performed at line rates after performing the compression through these techniques (Qi et al., 2011). Moreover, designing memories with such huge memory bandwidth is not practically achievable. To address the problem of efficient transition compression and performing signature matching at line rates, various bitmap-based transition compression techniques (Qi et al., 2011; Wang et al., 2011) have been proposed in the literature. However, the usage of bitmaps to compress the redundant state transitions also requires the bitmap to be stored in the memory along with the compressed state transitions. So, the existing bitmap-based methods compromise on the transition compression rates and only achieve compression rates of the order of 90-95%, primarily to minimize the number of bitmaps stored in the memory. However, this approach increases the memory footprint of the compressed DFA and results in inefficient usage of on-chip memories (Subramanian et al., 2016). Addressing this problem, the Member State Bitmask Technique and the Leader State Compression Technique were proposed, in which an additional layer of indexing called bitmask was introduced to improve the achievable transition compression rates to over 98% (Subramanian et al., 2016). The improved transition compression resulted in a 50% reduction in the memory footprint of the compressed DFA in comparison to the existing methods. Moreover, in addition to the transition compression methods, Subramanian et al. (2016) also proposed a corresponding hardware accelerator to perform line-rate signature matching. Extending the idea proposed in Subramanian et al. (2016), this paper further discusses the structural hardware building blocks which are required to perform the transition decompression at line rates through a hardware accelerator. A software model of the transition decompression engines was designed to verify the compression algorithms and was evaluated with synthetic traffic workloads spanning across different levels of maliciousness. The signature matching results extracted from the software model were identical to that of the DFA-based signature matching engine, further validating the correctness of the compression methods. Moreover, this paper discusses and evaluates additional optimization steps in the transition decompression process to further improve the per-stream signature matching throughput that can be achieved through the hardware accelerator. Experimental evaluations further show that the proposed optimizations result in 1.25–1.4x improvement in the per-stream signature matching throughput in comparison to the per-stream throughput without the optimizations.

2. Prior Art and Key Contributions

2.1 Introduction to DFA

If Sˈ represents the set of ‘N’ DFA states and Cˈ represents the set of characters, each entry in the DFA stores the state transition δ(s, c) = t, where s, t  Sˈ represents the current state and the next state, respectively; c  Cˈ represents the character; and δ represents the state transition function. The total number of state transitions generated in the DFA is a product of the total number of states generated and the number of characters for which the transitions are represented in a state as shown in (1).

If the DFA is directly stored in the memory, the amount of memory required to store the DFA corresponds to the memory required to store all the state transitions as shown in (1). However, only a very small portion of the transitions in a DFA lead to a successful signature, while the majority of others do not. These transitions which do not lead to a signature match are called the failure transitions. Many of these failure transitions are redundant and compressing these transitions enables efficient storage of the DFA. As mentioned previously, the transition compression techniques which are used to compress these redundant transitions can be broadly classified into software- and hardware-oriented techniques. Though the aim of both these techniques is to compress the redundant transitions in a DFA, the algorithmic approach towards transition compression in hardware-oriented techniques enables the decompression to be performed in a dedicated hardware accelerator, which is not possible in the case of software-oriented solutions (Qi et al., 2011).

2.2. Software-Oriented Transition Compression Techniques

Kumar et al. (2006) identified equivalent transitions between states in a DFA, which are compressed by introducing a default transition to create a D²FA. However, the default transition paths can be very long, which in turn results in multiple memory lookups to fetch a compressed transition. To avoid the long default path, Becchi and Crowley (2007a, 2013), proposed the Amortized time-bandwidth overhead DFA (A-DFA) with directional default path selection. This approach reduced the length of the default paths, but also reduced the transition compression achieved in certain cases. However, in both D²FA and A-DFA, the compressed transitions in a state have to be sequentially searched, which further leads to additional memory lookups. Analysis in Qi et al. (2011) identified that the average number of transitions traversed to identify the next state is about 100 per input character using the D²FA and A-DFA compression algorithms. To avoid this problem, δFA (Ficara et al., 2008) was proposed, which only stored those transitions in a state that were different from its parent state. δFA also defined how to identify the parent state for a state whose transitions are compressed. Transitions corresponding to the character set are periodically updated in a local cache as the states are traversed through. Even though the local cache memory is used to store the transitions, the cache has to be frequently updated and the frequency depends on whether a transition is fetched from the parent state or not. The average transition compression rates achieved by D²FA, A-DFA and δFA are typically of the order of about 90% (Xu, 2016). Rafael et al. (2015) identified that a large set of transitions in a state are directed to a same next state and can be compressed by representing them as a ranged transition representation and defined the Ranged Compressed Deterministic Finite Automata (RCDFA). The RCDFA achieved transition compression rates of the order of 97% and, in turn, resulted in fewer transitions stored per state in comparison to the other proposals discussed above. The signature matching throughput that could be achieved by the various methods described above was compared in Rafael et al. (2015)[i]. The signature matching throughput achieved when the payload was compared against the uncompressed DFA representation was used as the benchmark for comparison purposes. The average signature matching throughput achieved by the DFA-based (uncompressed) signature matching engine was ∼400 Mbps. On the other hand, the average signature matching throughput achieved through the A-DFA and the RCDFA implementations was of the order of 10 Mbps and 200 Mbps, respectively. It was pointed out in the evaluation that the reduction in the signature matching throughput was due to the sequential fetch of additional state transitions as part of the decompression process. Moreover, Qi et al. (2011) pointed out that multiple terabits of on-chip memory bandwidth are required to support line-rate signature matching in methods such as D²FA and A-DFA.

2.3. Hardware-Oriented Transition Compression Techniques

Hardware-oriented transition compression techniques can be classified into hash-based and bitmap-based techniques (Subramanian et al., 2016). Hash-based solutions identify and store the non-redundant transitions in a DFA in a hash table by using the current state and character as hash keys. A hash-based technique was proposed in Lunteren & Guanella (2012) where the DFA transitions are converted into rules which are stored in the memory. There can be multiple rules associated with every unique transition and all of them have to be stored in on-chip memory. As the number of signatures increases, the number of customized rules also increases, which are eventually stored in the off-chip DRAM. The latency associated with a rule fetch from the DRAM reduces the signature matching throughput affecting the scalability of the solution. In worst case scenarios, the throughput achieved by the solution dropped to 2 Gbps, while the maximum throughput that can be achieved by the solution is 73.6 Gbps.

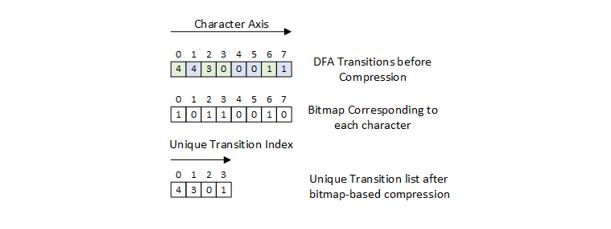
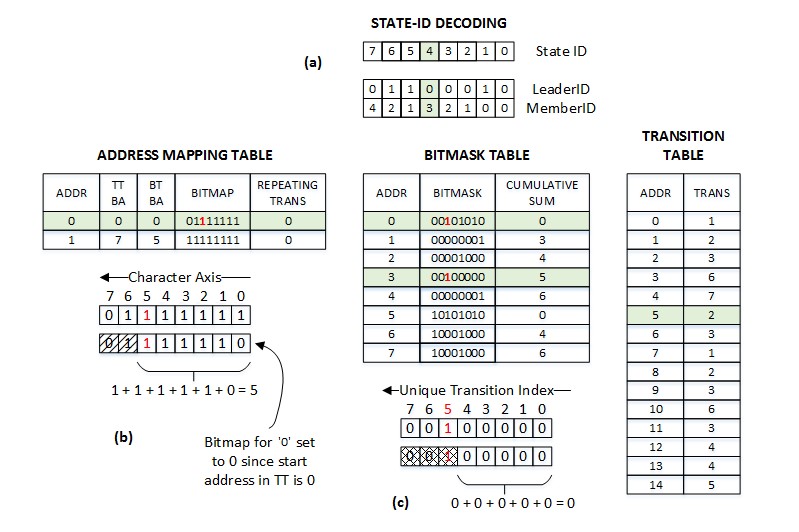
On the other hand, bitmap-based techniques compress adjacent transitions that are identical to each other in a DFA and a bitmap is used to identify the transition indices which have been compressed. For example, a K-bit bitmap is used to identify if a transition is compressed or not in a sequence of K state transitions. An index ‘i’ in the K-bit bitmap has a ‘0’ stored, if the transition corresponding to that index is compressed. On the other hand, the index has a ‘1’, to identify a transition that is not compressed. The transitions that are not compressed are stored in a unique transition list with a unique transition index to identify their location. The unique transition index corresponding to a transition can be found by calculating the number of 1’s in the bitmap before the index of interest until the least significant bit position. Figure 1 shows a transition sequence with 8 transitions. The transitions corresponding to indices 1, 4, 5 and 7 represented in blue are compressed, while the ones represented in green are uncompressed. The bitmap corresponding to each character is shown, along with the unique transition list, in Figure 1.

Figure 1. Example of a bitmap and a unique transition list.

Reorganized and Compact DFA (RCDFA) (Wang et al., 2011) is a bitmap-based transition compression technique which performs bitmap-based compression along the state axis. The RCDFA originally achieves transition compression rates of the order of 97-98%. However, in order to reduce the number of bitmaps stored in the memory, RCDFA stores additional redundant state transitions, which reduces the compression rates to 95%, resulting in an increased overall memory footprint of the compressed DFA.  

Another bitmap-based transition compression technique is proposed in Qi et al. (2011), which achieves transition compression of the order of about 90% by grouping states and is called Front-End Acceleration for Content-Aware Network processing (FEACAN). This technique observes both intra-state as well as inter-state transition redundancy in a DFA. The intra-state redundancy is removed by compressing the transitions using bitmap along the character axis. For example (see Figure 2(a)), the state transitions corresponding to the index in character 7 is compressed in states 0, 2, 3, 4 and 7 since it is identical to that of character 6. The inter-state redundancy is removed by grouping the states into subsets and by comparing the compressed transitions within the state groups. After state grouping, one of the states in the group is referred to as the leader state and all other states in the group are called the member states. After the state grouping, a comparison is made at each unique transition index between the leader transition and all the member transitions. Member transitions corresponding to each unique transition index are compressed, if and only if all of them are identical to the leader transition. This step removes inter-state redundancy. Figure 2(a) shows a DFA with 8 states and 8 characters and Figure 2(b) shows the DFA after the bitmap-based intra-state compression step, while Figure 2(c) shows the compressed DFA after inter-state compression. The transitions shown in red in Figure 2(c) are the redundant ones which are stored in memory, even though they are the same as the leader transition. It can be seen from Figure 2(c) that only 33 out of 64 transitions are compressed using the above-mentioned compression algorithm. Both the compression algorithms discussed above propose a hardware-based decompression engine to achieve signature matching at multi gigabit rates.

Figure 2. (a) An Example of a DFA with 8 states and 8 characters; (b) Compressed DFA after bitmap-based compression in the character axis and state grouping; (c) Compressed DFA after intra-state and inter-state compression.

To summarize, the memory components in bitmap-based techniques can be split into control and transition memories. The transition compression rates achieved through the bitmap-based techniques are around 90% in the case of FEACAN and 95% in the case of RCDFA. Thus, the resulting transition compression rates result in inefficient storage of the compressed DFA in the on-chip memories.

2.4. Key Contributions

The state-of-the-art bitmap-based compression techniques do not result in efficient transition compression, leading to inefficient usage of on-chip memories to store the compressed transitions. This can either be due to the algorithmic limitations as in the case of Qi et al. (2011) or the redundant transitions being stored to reduce the number of unique bitmaps stored in memory, as in the case of Wang et al. (2011). Addressing these weaknesses, two bitmap-based transition compression techniques, the Member State Bitmask Technique (MSBT) and the Leader State Compression Technique (LSCT) were proposed in Subramanian et al. (2016). The key idea behind these two techniques is an additional level of indexing with the introduction of bitmasks, which efficiently index the non-redundant transitions after bitmap-based transition compression. The additional indexing not only results in a reduced transition memory usage, but also reduces the overall memory usage to store the compressed transitions. This paper describes an extension of the MSBT and LSCT ideas with the following key contributions:

• This paper proposes the key hardware building blocks for the decompression system using the proposed MSBT and the LSCT compression methodologies. Additionally, this paper proposes and evaluates the theoretical relationship between the best- and the worst-case throughput that can be achieved by the MSBT and LSCT based hardware decompression engines and the number of pipeline stages associated with the hardware engines. The experimental evaluation of the optimizations introduced in the hardware accelerator shows further increases in the per-stream signature matching throughput by a factor of 1.2 to 1.4x.
• This paper details the validation of the software model of the proposed transition decompression engines. The software model of the decompression engines is validated by injecting 1 MB of synthetic traffic of various maliciousness levels. The identical signature matching results between the proposed models and the DFA further validate the functional correctness of the proposed methods.

3. Member State Bitmask Technique

3.1. Masking the Redundant Member Transitions – Member Transition Bitmask

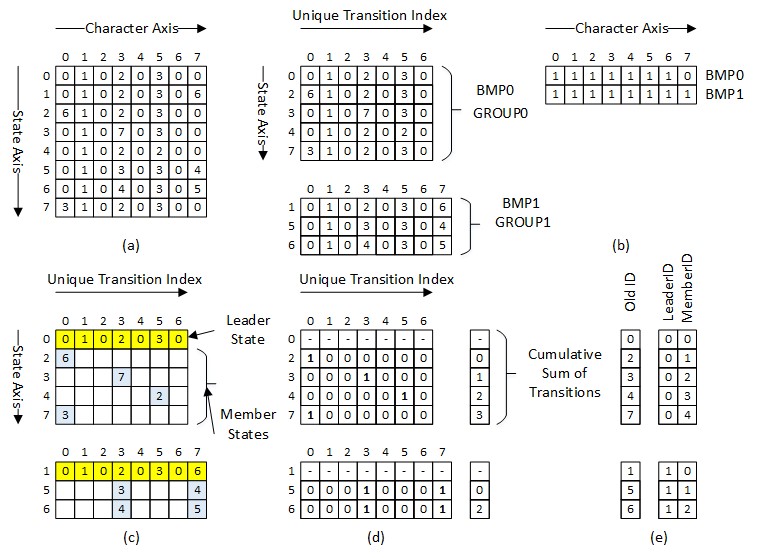
MSBT is a two-dimensional transition compression technique that performs intra-state and inter-state transition compression. The intra-state redundant transitions are compressed along the character axis through bitmaps and the compressed states are grouped into subsets of states. The state grouping algorithm proposed in Qi et al. (2011) is used for state grouping. States which share the same bitmap and a certain percentage of identical transitions, defined by the transition threshold, are clustered into a group. After grouping the states into subsets of states, a leader state is identified for each group, while the rest of the states are called the member states. As part of the inter-state compression, the transitions in a member state that are identical to the transitions in a leader state at each unique transition index are compressed. The member transition which is not identical to that of the leader transition in a member state can be identified using a Member Transition Bitmask (MTB) for each of the member states. The MTB is composed of a sequence of mask bits, where each bit corresponds to a unique transition index and represents whether a member transition at an index is identical or different in comparison to the leader transition at the same index. If the member and leader transitions are identical at the unique transition index, then the bitmask bit corresponding to the index is marked ‘0’ in the MTB. If not, the bitmask bit for the index is marked ‘1’ in the MTB.

Figure 3. (a) Original DFA before compression; (b) Compressed DFA after bitmap-based intra-state compression and state grouping; (c) Compressed DFA after MSBT; (d) Member Transition Bitmask for each member state; (e) Encoded State representation after MSBT.

Figure 3(a) shows the original DFA before transition compression and Figure 3(b) shows the DFA after the intra-state compression and the state grouping step. Figure 3(d) shows the MTB for each member state in a group. Figure 3(c) shows the compressed transitions after the inter-state compression step. For example, the bitmask bit at index ‘0’ for state ‘2’ has a ‘1’, representing that the member transition at the index is different from the leader transition at the same index. On the other hand, the bitmask bit at index ‘3’ for the state ‘2’ has a ‘0’, representing that the member transition at the index is the same as the leader transition at the same index. It can be seen from Figure 3(c) that 41[ii] transitions are compressed using the MSBT compression in comparison to 33 transitions that were compressed as shown in Figure 2(c) using the same reference DFA. The transitions which remain uncompressed in the leader state are shown in yellow and the transitions which remain uncompressed in the member states are shown in blue in Figure 3(c). These are the transitions which are stored in memory after implementing the MSBT-based transition compression.

If a DFA is compressed using the MSBT, a next state transition can be decompressed in the following way. If the current state is a leader state, then the transition at the unique transition index corresponding to the incoming character is directly assigned as the next state. If the current state is a member state, the bitmask bit corresponding to the unique transition index decides the next state. If the bitmask bit at the unique transition index is a ‘1’, the member transition which remains uncompressed corresponding to the unique transition index is assigned as the next state. If the bitmask bit corresponding to the unique transition index is a ‘0’, the leader transition corresponding to the unique transition index is chosen as the next state.

The cost paid for the additional compression is the memory used to store the MTB. The maximum width of the unique transition index for a group defines the length of the MTB. For example, the maximum width of the unique transition index corresponding to group ‘0’ is 7, resulting in a 7-bit MTB for each member state in the group. A cumulative sum of all member transitions, which remain uncompressed until each member state in a group is stored in the memory along with the MTBs, is shown in Figure 3(d). For example, a cumulative sum of ‘3’, corresponding to state 7 represents that 3 member transitions are stored in memory before the first uncompressed member transition belonging to state 7 is stored.

In the MSBT, the states are encoded and represented as a combination of leaderID and memberID similar to the state encoding technique used in Qi et al. (2011). Figure 3(e) shows the state encoding between the two representations. The leaderID identifies the group to which a state belongs and the memberID identifies the member representation within a group of states. The memberID for the leader state is always kept ‘0’ to easily differentiate between a leader state and other member states.

3.2. Functional Description of the Hardware Decompression Engine (MSBT)

3.2.1. Components of the Hardware Decompression Engine

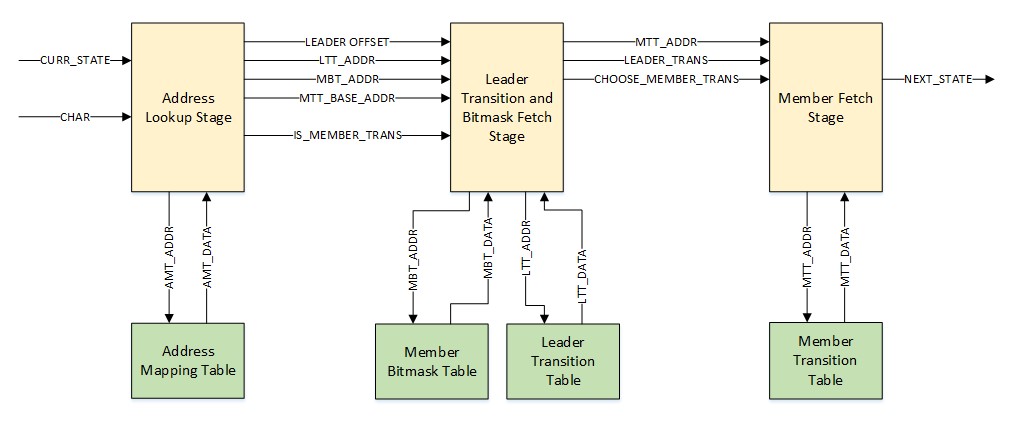
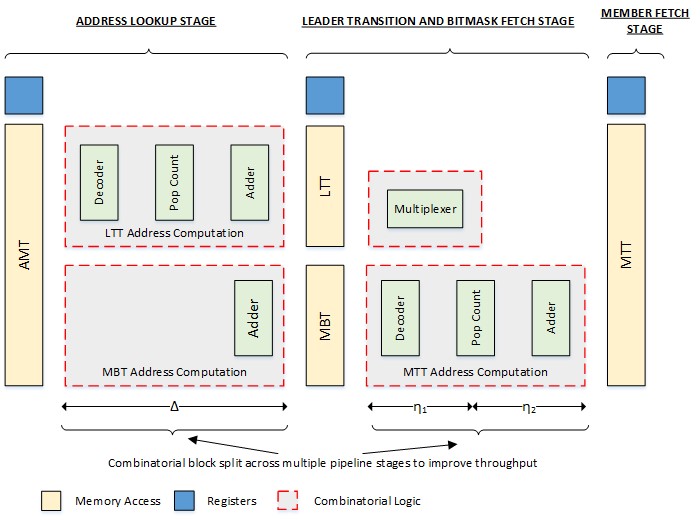
A hardware acceleration engine is proposed to decompress the transitions that are compressed using the MSBT. Figure 4 shows the functional architecture of the signature matching engine. The engine is split across three processing stages, to include the Address Lookup Stage (ALS), the Leader Transition and Bitmask Fetch Stage (LTBFS) and the Member Fetch Stage (MFS). There are four lookup tables across which the compressed transitions and the control information are split. The Leader Transition Table (LTT) belongs to the second stage and stores the transitions which remain uncompressed after the bitmap-based compression among the leader states. The Member Bitmask Table (MBT) also belongs to the second stage and stores the MTB for each member state along with the cumulative sum of transitions. The Member Transition Table (MTT) belongs to the third stage and stores the member transitions which remain uncompressed after the intra- and inter-state compression. The Address Mapping Table (AMT) belongs to the first stage and stores the address location of the first transition in LTT, MTT and the first MTB for each group, which are referred to as LTT base address, MTT base address and MTB base address, respectively. The AMT also stores the bitmap for each group.

Figure 4. Functional description of the hardware-based decompression architecture for MSBT.

3.2.2. How to Fetch a Compressed Transition

The current state and the incoming character are passed as inputs to the first stage to compute the leader offset, the address location for LTT and MBT based on the data fetched from the AMT. As mentioned earlier, the DFA state is represented as a combination of the leaderID and the memberID after compression. The leaderID is used as the address to fetch the information from the AMT. The leader offset identifies the unique transition index corresponding to the character. The leader offset can be calculated by computing the total number of 1’s in the bitmap from the least significant bit position to the position before the character. The LTT base address fetched from the AMT is added together with the leader offset to generate the address location for the LTT. The MTB base address fetched from AMT is added together with ‘memberID-1’ to generate the address location for the MBT.  

The second stage uses the addresses calculated in the first stage to fetch the data from the LTT and the MBT. The bitmask bit corresponding to the leader offset position in the MTB will identify if the member state transition is compressed. If the current state is a member state and the bitmask bit corresponding to the leader offset is ‘1’, a member offset is calculated. The member offset is calculated by computing the total 1’s in the MTB from the least significant bit position to the position before the leader offset. The member offset identifies the relative position of a transition in the member state with respect to its first transition that remains uncompressed. The member offset information when added together with the cumulative sum provides the relative position of a transition that remains uncompressed in the group. This information is added together with the MTT base address to generate the address location for the transition in the MTT. The third stage takes the generated leader transition and the MTT address location as inputs. The next state assignment is multiplexed between the transition fetched from the LTT and the transition fetched from the MTT depending on the bitmask bit corresponding to the leader offset and the current state, as discussed previously.   

All memories used in the MSBT implementation are single port memories and can be categorized into control and transition memories. AMT and MBT belong to the control memories, as they store the control information such as the base addresses, the bitmaps and the bitmasks which are used to compute the location of a compressed transition. On the other hand, the LTT and the MTT are transition memories as they actually store the compressed state transitions. The basic idea of the proposal is to store more information in the control memory in comparison to the state-of-the-art implementations to improve the transition compression, resulting in an overall reduction in the memory usage.

3.2.3. Example of a Transition Fetch

Figure 5 illustrates the various tables explained above with respect to the compressed DFA shown in Figure 3(c). To maintain simplicity with the representation of the transitions in the transition memories, the encoded representation is not shown in Figure 5. The addresses and the state ID’s are represented as decimal numbers. Moreover, the bitmap and the MTB have been represented in the binary format with the least significant bit on the right, which denotes the index with the least value.

Figure 5. Representation of the compressed DFA with respect to MSBT decompression system.

The transition fetch for a state character combination of ‘4’ and ‘5’ is used as an example to explain the decompression process. The information fetched from various memories is highlighted in green, while the bits of interest in the bitmap and the bitmask are highlighted in red in Figure 5. The leaderID corresponding to state 4 is ‘0’ and is used as the address to fetch the data from the AMT. The bitmap bit corresponding to character ‘5’ is ‘1’ and, in turn, the computed leader offset is ‘5’. The LTT base address value of ‘0’ is fetched from the AMT which, when added to the leader offset, generates ‘5’ as the LTT address location. Since the state ‘4’ is a member state in group 0, the bitmask bit at the leader offset position is checked to identify whether the next state is assigned from the LTT or the MTT. Since the bitmask bit at the leader offset position is ‘1’, the transition fetched from the MTT is assigned as the next state. In this case, since both the MTT base address and the member offset are ‘0’ and the cumulative sum of transitions is 2, the computed MTT address location is ‘2’. The transition fetched from MTT address location ‘2’ is ‘2’, which exactly matches the transition corresponding to the state character combination seen in Figure 3(a).

4. Leader State Compression Technique

4.1. Compressing the Most Repeated Leader Transitions – Leader Transition Bitmask

Bitmap-based intra-state transition compression can effectively compress transitions which are identical and at the same time adjacent to each other. Even after bitmap-based compression, there are certain transitions in the unique transition list which have the same transition entry, but cannot be compressed, just because they are not contiguous. During the MSBT-based compression, if these transitions belong to a member state, there is a chance of them being compressed during the inter-state compression step. On the other hand, if these transitions belong to a leader state, they cannot be compressed at all. Specifically, this scenario occurs in the case of failure transitions belonging to a leader state. These failure transitions can be spread across the character axis and can be blocked by those transitions which lead to a forward match in a signature. For example, after the MSBT, the leader state ‘0’ corresponding to group ‘0’ shown in Figure 3(c) has transition ‘0’ at unique transition indices 0, 2, 4 and 6. Even though these transitions are exactly the same, they are not compressed as they are not adjacent to each other. Based on our observation, on average about 40% of the transitions in the unique transition list among the leader states converge to a same next state and are not compressed because of the reasons explained above.

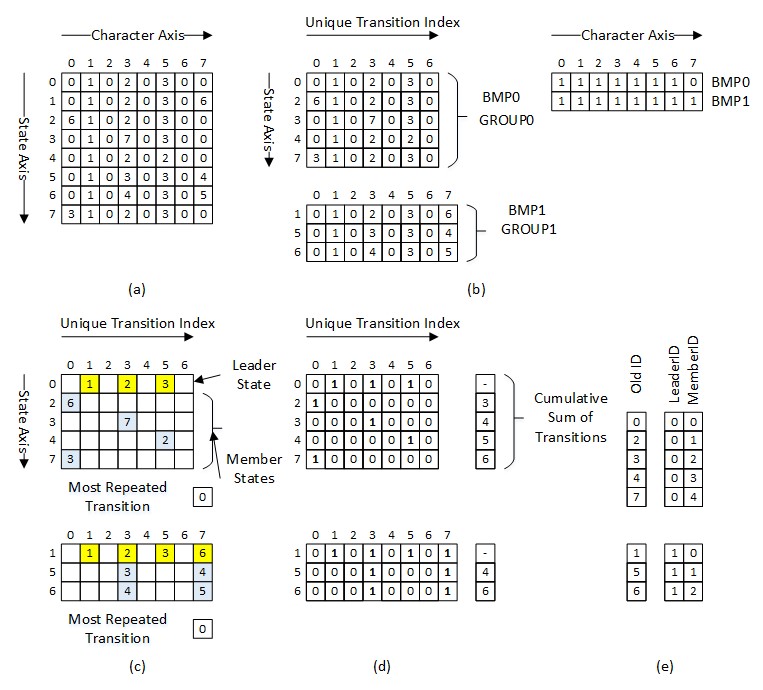
In order to reduce the redundancy in the leader state unique transition list, as discussed above, an efficient method is proposed to index a single most repeated transition through the Leader Transition Bitmask (LTB). The single most repeated transition can be identified by sorting all the transitions in the unique transition list based on the frequency of their occurrence using sorting algorithms such as the quick sort (Cormen et al., 2009). After identifying the single most repeated transition, a single bit at each unique transition index position is used to distinguish the indices with the most repeated transition in the leader state. An index position with the most repeated transition is represented with a ‘0’; and a ‘1’ if not. The most repeated transition is stored only once, while the transitions that differ remain uncompressed and are stored in the memory. The proposed LTB can be combined with the MSBT. The LTB is introduced after the inter-state compression step in the MSBT and brings additional compression to a DFA. This methodology of compressing the repeated leader transitions together with MSBT is called the Leader State Compression Technique (LSCT).

Figure 6. (a) Original DFA before compression; (b) Compressed DFA after bitmap-based intra-state compression and state grouping; (c) Compressed DFA after LSCT; (d) Member Transition Bitmask and Leader Transition Bitmask for each state; (e) Encoded State representation after MSBT.

Figure 6(a) shows the original DFA and Figure 6(b) shows the DFA after the intra-state compression by using bitmaps and state grouping. Figure 6(c) shows the compressed DFA after the intra-state and inter-state compression based on the LSCT. It can be seen that a total of 47[iii] transitions are compressed using LSCT, while only 41 transitions were compressed using MSBT, as shown in Figure 3(c). Transitions represented in yellow are those leader transitions which remain uncompressed, while the transitions represented in blue are those member transitions which remain uncompressed after the LSCT. The LTB and the MTBs corresponding to the leader and member states are shown in Figure 6(d). For example, the entry corresponding to the unique transition index ‘2’ in group ‘0’ has a ‘0’ which represents that the leader transition corresponding to the entry is the most repeated transition. On the other hand, the entry corresponding to the unique transition index ‘3’ in group ‘0’ has a ‘1’ representing that the leader transition corresponding to the entry is not the most repeated transition.

If a DFA is compressed using the LSCT, the next state transition can be decompressed in the following way. If the current state is a leader state, then the bitmask bit corresponding to the unique transition index in the LTB is calculated. If the bitmask bit is ‘0’, then the most repeated transition is assigned as the next state. If the bitmask bit is ‘1’, then the leader transition which remains uncompressed corresponding to the unique transition index is assigned as the next state. If the current state is a member state, the bitmask bit corresponding to the unique transition index in the MTB is identified. If the bitmask bit is ‘0’, then the same procedure is followed as in the case of the leader state. If the bitmask bit is ‘1’, then the member transition which remains uncompressed corresponding to the unique transition index is assigned as the next state.

4.2. Functional Description of the Hardware Decompression Engine (LSCT)

4.2.1. Components of the Hardware Decompression Engine

Figure 7. Functional description of the hardware-based decompression architecture for LSCT.

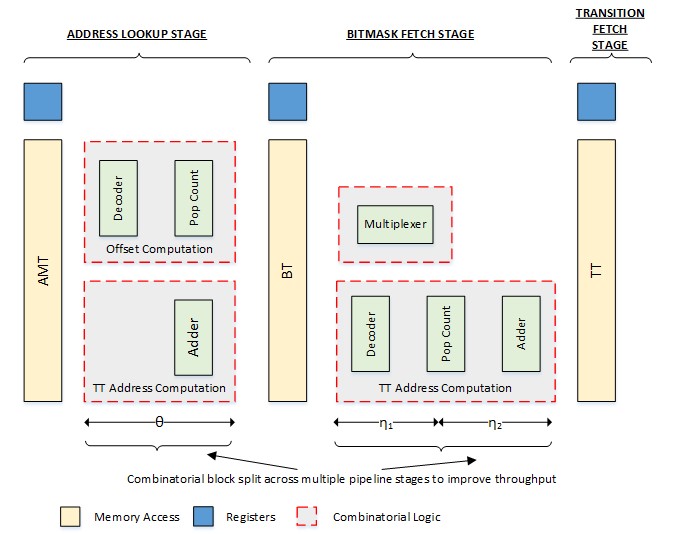
A hardware acceleration architecture is proposed to decompress the transitions which are compressed using the LSCT. Figure 7 shows the functional architecture of the signature matching engine. The engine is split across three processing stages, to include the Address Lookup Stage (ALS), the Bitmask Fetch Stage (BFS) and the Transition Fetch Stage (TFS), respectively. The transitions which remain uncompressed and the control information are split across three lookup tables. The Bitmask Table (BT) belongs to the second stage and stores the LTB in the case of the leader state and the MTB in the case of a member state, along with the cumulative sum of transitions for each state. Unlike the MSBT, the BT in LSCT is implemented using a dual port memory, as both the MTB and the LTB have to be fetched simultaneously. The Transition Table (TT) belongs to the third stage and stores the leader and the member transitions that remain uncompressed after the intra- and inter-state compression. The Address Mapping Table (AMT) belongs to the first stage and stores the base address of the first transition that remains uncompressed and the first bitmask for each group. These are referred to as TT base address and BT base address, respectively. The AMT also stores the bitmap for each of the groups and the most repeated transition in the leader state. Similar to the MSBT, the AMT and BT are the control memories and TT is the transition memory.

4.2.2. How to Fetch a Compressed Transition

The current state and the incoming character are passed as inputs to the first stage to compute the leader offset and the address location to fetch the LTB and the MTB (BT_LTB_ADDR & BT_MTB_ADDR). The leaderID (which is part of the state encoding) corresponding to the current state is used as the address to fetch the data from the AMT. The leader offset is calculated analogous to how the leader offset was computed in the case of MSBT. The BT base address represents the address from which the LTB is fetched. The memberID when added to the BT base address provides the address from which the MTB and the cumulative sum of transitions are fetched. The first stage also provides the TT base address and the most repeated transition as inputs to the second stage.   

The addresses generated by the first stage are used to fetch the LTB and the MTB from the BT simultaneously. The bitmask bit corresponding to the leader offset is checked in both the LTB and MTB; these bits are denoted as the leader bitmask bit and the member bitmask bit. If the current state is a leader state and the leader bitmask bit is ‘1’ or if the current state is a member state and the member bitmask bit is ‘0’, a transition offset is calculated similar to the member offset calculation in the case of MSBT. The transition offset is then added together with the TT base address to generate the TT address location. On the other hand, if the current state is a member state and the member bitmask bit is ‘1’, the transition offset which is calculated is added together with the cumulative sum of transitions and the TT base address to generate the TT address location. If the current state is a member state and both the leader bitmask bit and the member bitmask bit are ‘0’ or if the current state is a leader state and the leader bitmask is ‘0’, then there is no need for any address computation as the most repeated transition can be assigned as the next state. The second stage provides the information on when the generated address can be used for TT to the third stage based on the above combinations.

The third stage takes the generated TT address, the most repeated transition and assigns the compressed state transitions depending on the bitmasks. The transition is fetched from the generated TT address and the next state is multiplexed between the transition fetched from TT and the most repeated transition based on the combinations discussed above.

Figure 8. Representation of the compressed DFA with respect to MSBT decompression system.

4.2.3. Example of a Transition Fetch

Figure 8 illustrates the various tables explained above with respect to the compressed DFA shown in Figure 6(c). Similar to the example shown for MSBT, the decimal numbers are used to represent the addresses and transitions. The bitmap and the MTB have been represented in binary format with the least significant bit on the right, which denotes the index with the least value. The transition fetch for a state character combination of ‘4’ and ‘5’ respectively is shown as an example to explain the decompression based on the LSCT compression. The information fetched from various memories is highlighted in green, while the bits of interest in the bitmap and the bitmask are highlighted in red in Figure 8.

The leaderID corresponding to state 4 is ‘0’ and is used as the address to fetch the data from the AMT. The bitmap bit corresponding to the character is ‘1’ as calculated from the bitmap, which results in the leader offset of ‘5’. Since state 4 is a member state in group ‘0’, the LTB and the MTB are fetched from address locations ‘0’ and ‘3’, respectively. Both the leader bitmask bit and the member bitmask bit corresponding to leader offset ‘5’ are calculated to be ‘1’. Since the current state is a member state, the member bitmask bit takes priority, which represents that the transition corresponding to the state character combination is not compressed. The TT address from which the compressed transition is fetched is calculated to be ‘5’, since both the transition offset and the TT base address are ‘0’. The transition ‘2’, which is fetched from TT address location ‘5’, is the same as seen in the uncompressed DFA shown in Figure 6(a). 

Figure 9. Hardware building blocks for MSBT-based decompression system.

5. Considerations for Hardware Implementation

5.1. Hardware Building Blocks Description

Figures 9 and 10 show the hardware building blocks for the MSBT and the LSCT decompression engines, respectively. The memory accesses and the associated combinatorial blocks have been shown in yellow and grey blocks, respectively. For example, the address lookup stage in both Figures 9 and 10 consists of a single memory access for the AMT, followed by a combinatorial logic block which processes the data fetched from the memory to generate the addresses for the next stage. The same applies to all other functional blocks. Assuming that all the memories are clocked at the same frequency, it would take 3 clock cycles to decompress a transition based on the MSBT or the LSCT. Since there are 3 memory accesses that are part of the transition decompression, it would take a minimum of 3 clock cycles to determine the next state.

Figure 10. Hardware building blocks for LSCT-based decompression system.

The key combinatorial building blocks required for the hardware realization of the MSBT and the LSCT decompression can be classified into the decoder, the population count (Pop Count), the adder and the multiplexer blocks. The Pop Count block is used to compute the offsets from the bitmap or the bitmask by computing the total number of set bits (1’s) in an input vector. The pop-count block can be realized similar to the 64-bit Wallace tree structure proposed in Rajaraman et al. (2008). MSBT and the LSCT implementations require the pop-count to be performed on a 256-bit input vector to support the ASCII character set. So, the 64-bit structure proposed in the literature can be extended to a 256-bit structure. The decoder block masks the bits in the bitmap or the bitmask which have to be excluded from the pop-count computation based on the character or the leader offset position in the 256-bit vector. These are the bits from the position of interest, i.e. the character index in the case of the bitmap and the leader offset index in the case of the bitmask until the most significant bit position. Adder circuits such as the ones proposed in Zeydel, Baran & Oklobdzija (2010) can be used to achieve high speed and low power implementations in the address generation blocks. The multiplexer block chooses one of the 256 bits in the bitmap or the bitmask to identify the bitmap or the bitmask bit associated with an index. The multiplexer block can be constructed using multiple smaller multiplexers, for example 2 to 1 multiplexers in a logarithmic fashion using the binary tree topology.  

5.2. Pipelining vs Throughput

As mentioned in the previous section, each functional stage is a combination of a single memory lookup followed by a combinatorial function which processes the data from the memory. So, it would take 3 clock cycles for a transition to be decompressed from the memory. For example, if the character is consumed in the first clock cycle as an input, the subsequent character can only be consumed in the 4th clock cycle, as it takes 3 clock cycles to process the character and identify the next state corresponding to it. So, in order to keep the pipeline busy and to fully utilize the hardware resources, characters from multiple data streams can be interleaved as proposed in Basu & Narlikar (2005). Since there are 3 pipeline stages (corresponding to 3 memory accesses), characters from 3 different data streams are passed to the pipeline in an interleaved manner once every 3 clock cycles.

To generalize, if ‘P’ is assumed to be the total number of pipeline stages to process a character from one data stream, characters from ‘P’ different data streams have to be interleaved to extract the best from the hardware resources. Since each character corresponds to 8 bits and the system can consume one character every clock cycle, the throughput that can be achieved is a product of the frequency and the character width. Assuming F to be the frequency at which the system is clocked, the throughput T achieved by the decompression system can be generalized as shown in (2).

Since characters from multiple streams are input to effectively utilize the hardware resources, the maximum throughput that is achieved by one of the interleaved streams is inversely proportional to the number of pipeline stages. Equation (3) shows the maximum achievable throughput T_{stream_max_pipeline} for a single stream among the interleaved streams during pipelined operation. 

Based on (1), the throughput, T, can either be increased by increasing the clock frequency or increasing the character width, i.e., by sending multiple characters per stream per clock cycle. Processing multiple characters per stream requires the conversion of the DFA into a multi-stride DFA, which results in an exponential memory growth and is not a scalable approach (Becchi & Crowley, 2013). Thus, the only way in which the throughput can be improved is by increasing the operating frequency of the transition decompression. The frequency that can be achieved depends on two factors: the latency associated with the SRAM fetch; and the latency associated with the combinatorial processing path in the pipeline. The latency associated with the SRAM fetch can be optimized by effectively configuring the memories as part of the ASIC design flow. Similarly, the combinatorial processing logic associated with various functional stages can be broken down into multiple pipeline stages by introducing additional registers to increase the frequency of operation. On the contrary, splitting the combinatorial path into pipelines will also reduce the maximum throughput that can be achieved by a single stream, since they are inversely proportional to each other, as shown in (3).

In the case of the MSBT and the LSCT, the number of pipeline stages required to process an incoming character can be broken down into a fixed and a variable count. The former is the number of pipeline stages which is a bare minimum requirement due to the associated memory fetches. In both the MSBT and the LSCT, the fixed pipeline stage count is 3, as there are 3 memory fetches as part of the transition decompression. The latter is a variable component, which results from the combinatorial block in each stage being split into multiple smaller stages to improve the clock frequency. In the case of the MSBT and the LSCT, the variable pipeline stage counts for the first stage are defined as Δ and θ, respectively. For example, if the combinatorial block in the ALS is split into 3 (Δ) stages, it would take 4 pipeline stages (3 (Δ) + 1 stage for AMT lookup) in the MSBT to finish the processing associated with the ALS. On the other hand, in the MSBT and the LSCT, the variable pipeline count associated with the second stage is defined by η, as the processing associated with these stages is exactly the same. Equations (4) and (5), respectively, define the total pipeline stage count P_MSBT and P_LSCT for MSBT and LSCT after design pipelining.

Providing multiple streams to the system is a best-case scenario to completely utilize the hardware resources. In the worst-case scenario, when only one stream is available to the pipeline, the maximum throughput that can be achieved is the same as described in (3). In this scenario, the throughput of the signature matching engine can be increased by directly assigning the next state from the transition fetched from the second functional stage whenever possible. This can happen in the case of MSBT, when the next state transition can be assigned from the transition fetched from the LTT. Similarly, in the case of LSCT, the most repeated leader state transition can be assigned as the next state based on the bitmasks that are fetched in the second stage. However, it should be noted that this is highly dependent on the sequence of characters which are inspected as part of the data stream. Additional circuitry can be added in the hardware to consider this special scenario to achieve a higher throughput when compared with T_{stream_max_pipeline}. The number of variable pipeline stages η in the second stage is split into η₁ and η₂, where η₁ represents the number of pipeline stages required to decide if the next state can be assigned in the second stage, while η₂ represents the number pipeline stages required for address calculation for the third stage. So, the minimum number of pipeline stages for the MSBT and the LSCT are represented as P_{MSBT_min} and P_{LSCT_min}, as shown in (6) and (7), respectively. The fixed pipeline component in (6) and (7) is represented as 2, as there are only 2 memory accesses required to identify the next state.

P(c)_MSBT[iv] is defined as the probability of a transition fetch from the third functional stage assigned as the next state, when a sequence of M bytes is inspected by the MSBT decompression system. Equation (8) shows the throughput T_{stream_max_MSBT} that can be achieved by a single stream in the worst-case scenario in relation to the probability of the transition fetch. Since P_{MSBT_min} is smaller than P_MSBT, a higher throughput can be achieved when P(c)_MSBT is smaller. Equation (9) shows a similar relationship between T_{stream_max_LSCT} and the probability of a transition fetched from the third functional stage P(c)_LSCT being assigned as the next state. Since the transitions which differ from the most repeated leader transitions are also stored in the TT, which belongs to the third stage, P(c)_LSCT will be higher than P(c)_MSBT for the same character sequence. Similar to MSBT, a higher throughput will be achieved in the case of LSCT when P(c)_LSCT is small.

6. Results and Discussion

This section analyses the compressed DFA resulting from the MSBT and the LSCT techniques in comparison to various other techniques discussed in the literature. The results section is split into two sub-sections to discuss the effectiveness of the transition compression techniques. The first section describes the experimental evaluation of the proposed techniques. The transition compression achieved using the proposed techniques is compared with A-DFA and FEACAN. The A-DFA and FEACAN are chosen as they represent the state-of-the-art software and the hardware-oriented compression techniques, respectively. This section also compares the memory used to store the compressed DFA in comparison to FEACAN. On the other hand, the second section describes the software simulation setup used to verify the functional correctness of the compression methods. This section further analyses the throughput of the decompression system based on the traffic generated with different levels of maliciousness.

6.1. Experimental Evaluation

A compiler was developed which takes the DFA as an input to generate the compressed transitions along with the control information such as the bitmaps and bitmasks as outputs. The maximum number of states in a group was restricted to 256 states and the transition threshold used for inter-state compression was set to 80%. The same set of states is used as inputs for all the three bitmap-based compression techniques. The compression algorithm was implemented in a Xeon server machine running at 4.4 GHz with 500 GB of main memory.

As proof of concept, the compression scheme was evaluated on DFAs generated across 5 different rule-sets listed in Table 1. The rule-sets were carefully identified to contain both strings and regular expression signatures. Exact match is a group of 500 string signatures synthetically generated from the tool developed by Becchi (2016). The other four rule-sets are extracted from Snort (Roesch, 1999) and Bro (Paxson, 1999) intrusion detection systems, respectively, and are a combination of simple strings and complex regular expressions. The signature sets were converted into the DFA using the regex tool (Becchi, 2016) and the custom compiler performs the MSBT and the LSCT on the generated DFAs. Column 3 in Table 1 presents the total DFA states generated, while columns 5 and 6 present the total leader states and member states after state grouping. Column 4 presents the total number of uncompressed transitions in the DFA.

Table 1. Rulesets Used in Simulations

Signature Set

#Signatures

#DFA States

#Transitions

#Leader States

#Member States

6.1.1. Transition Compression Ratio

The transition compression ratio is the ratio of the number of transitions that remain uncompressed to the number of transitions in the original DFA. Figure 11 compares the transition compression achieved by MSBT and LSCT in comparison to the theoretical maximum compression limit. Along with these, the transition compression results are compared across A-DFA and FEACAN as well. The parameters used for the A-DFA algorithm were tuned to achieve the best compression results.

The MSBT clearly shows an improvement of the order of 4-5% in the transition compression when compared with FEACAN. The improvement is a direct consequence of using MTBs to index the position of the redundant member transitions. The MTBs introduced as part of the MSBT index the redundant transitions in the member state which are not stored in the memory. Table 2 compares the average number of transitions that remain uncompressed in a member state after compressing the DFA using FEACAN and the MSBT. The information in Table 3 is extracted from the compilation results after performing the MSBT and the FEACAN compression on the signature sets described in Table 1. It can be seen that about 50 to 80% of the member transitions stored in FEACAN are redundant and can be compressed efficiently through the introduction of MTBs in the MSBT.

Figure 11. Comparison of transition compression across various techniques.

Table 2. Comparison of average number of transitions per member state after compression

Table 3. Comparison of average number of transitions per leader state after compression

A slight improvement in the transition compression is seen in the case of LSCT in comparison to MSBT as the most repeated leader transition for each leader state is compressed using the LTB. Table 3 shows the average number of leader transitions that remain uncompressed after the LSCT in comparison to the MSBT. The average number of transitions generated in the leader state is directly extracted from the compiler results after performing the MSBT and the LSCT on the described signature sets. It can be observed from Table 3 that 30-60% of the transitions in the leader are the single most repeated transitions and can be compressed effectively, which results in an increase in the transition compression.

The A-DFA achieves the best transition compression results when compared with all the other bitmap-based compression techniques and is also close to the theoretical limit. Table 4 shows a comparison of the average number of transitions which have to be fetched from the memory in each of the compression methods, before identifying the compressed state transition corresponding to a state character combination. The data in Table 4 was generated by directly analysing the compressed DFA generated through each of the techniques. A closer look at the results from Table 4 will detail the cost paid for the transition compression in the case of A-DFA. Columns 3, 4, 5 and 6 present the average number of transitions that have to be fetched from the memory to identify the compressed transition for A-DFA, FEACAN, MSBT and LSCT, respectively. Column 2 presents the maximum number of transitions that have to be fetched from the memory in the case of A-DFA before identifying the compressed transition. Columns 2 and 3 clearly show that multiple tens of transitions have to be fetched from memory before identifying the compressed transition corresponding to the state-character combination in the case of A-DFA. The sequential search associated with the software-oriented techniques such as A-DFA result in low signature matching throughput. The increased memory bandwidth is the cost paid by software-oriented solutions, such as A-DFA, to compress the redundant transitions. In the case of bitmap-based techniques, a maximum of 2 memory accesses is only required to fetch the compressed transition. The best-case scenario to identify the compressed transition is a single memory fetch in all cases. The ability to quickly fetch the compressed transition from the memory is a differentiating factor in bitmap-based transition compression techniques to achieve high throughput signature matching in comparison to software-oriented techniques. The numbers shown in columns 3 to 6 are average numbers to fetch a compressed transition extracted from the compressed automaton. These average numbers will vary based on access patterns in an automaton.

Table 4. Average number of transitions fetched before fetching the compressed transition

Table 5. Parameters Used for Memory Estimation

6.1.2. Memory Usage

Figure 12. Comparison of memory usage across various techniques.

Memory used to store the compressed automata is calculated by computing the sum of the memory used to store the compressed transitions and the memory used to store the control information, such as the base addresses, bitmaps and bitmasks. Table 5 lists the width of various information that is stored in memory as part of various techniques.

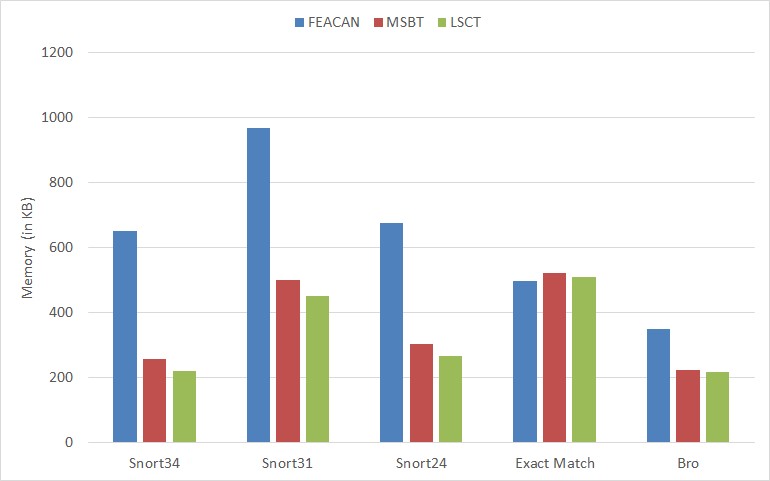
Figure 12 shows a comparison of the memory usage across different bitmap-based compression techniques. A small improvement of 4-5% in the transition compression ratio seen in Figure 11, in the case of MSBT, translates into an overall reduction in memory by 50% in most of the signature sets. Similarly, in the case of LSCT, even a very minute increase in the transition compression results in a significant 5–10% reduction in memory usage when compared with MSBT. Figure 13 shows a comparison of the transition and control memory usage across various techniques. As part of the control memory, FEACAN only stores the base addresses for the transition memories and the bitmap for certain groups of states. This represents a very negligible portion of the overall memory usage, while a major portion of the memory is used to store the compressed state transitions, as shown in Figure 13. On the other hand, in the case of MSBT and LSCT, a considerable portion of the overall memory is needed for the control memory to store the bitmasks, which in turn reduces the memory used by the transition memories. Even though storing the bitmasks for states increases the control portion of the memories, there is a huge reduction in the transition memory usage and also an overall reduction in the memory usage to store the compressed automata. As seen in Figures 12 and 13, Exact Match ruleset is an exception where the average length of the bitmask is 112 bits which, when stored per member state, needed a substantial portion of memory in comparison to other signature sets. The reduction in the transition memory which results by eliminating the redundant transitions in a member state is smaller in comparison to the memory used to store the bitmasks in case of the Exact Match ruleset. The average number of transitions per state after the intra-state compression directly corresponds to the length of the bitmask stored for a state. The memory used to store the compressed transitions in the case of software-based techniques such as A-DFA depends on the chosen memory layout (Chen et al., 2016) and is not compared with the proposed techniques.

Figure 13. Comparison of transition and control memory usage across various techniques.

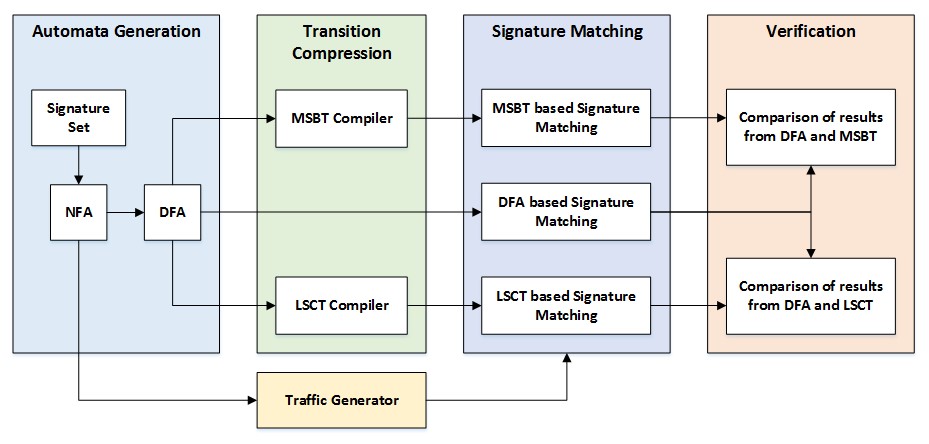
6.2. Simulation Setup

A software-based simulation was performed to verify the decompression system based on the MSBT and the LSCT compression. Figure 14 shows the overview of the software simulation setup. The signature sets were compiled into an NFA and a DFA using the regex tool (Becchi, 2016). The synthetic traffic generation module described by Michela, Mark & Patrick (2008), implemented in the regex tool, was used to generate the sequence of characters. The synthetic traffic generation module takes the NFA as an input and generates a sequence of characters, where each character in the sequence is decided based on a maliciousness probability P_M by traversing the NFA. The P_M value is the probability with which a forward transition is made for each character leading to a signature match. A lower P_M value indicates a lower probability of a successful signature match than a higher P_M value. Four different character sequences of 1 MB were generated based on the values chosen for P_M, which were 0.35, 0.55, 0.75 and 0.95. The DFA generated by the regex tool is used as an input to perform the transition compression using the MSBT and the LSCT compilers. A software model of the decompression system was developed for both the MSBT and the LSCT, which was used to perform signature matching on the compressed signatures. Table 6 shows a summary of the signature matching results obtained from the software model of the decompression systems and compares the results with a DFA-based signature matching engine across different signature sets and across the various P_M values. The identical signature matching results seen in Table 6 show the functional correctness of the proposed compression methods. In addition to tracking the total number of signature matches, as shown in Table 6, the next state transitions generated for each of the state character combinations were also monitored and the results were identical in all three systems across all the signatures sets across all the P_M values (not shown in the results section).

Figure 14. Overview of the software-based simulation environment to verify the decompression system.

6.2.1. Transition Fetch — Dynamic

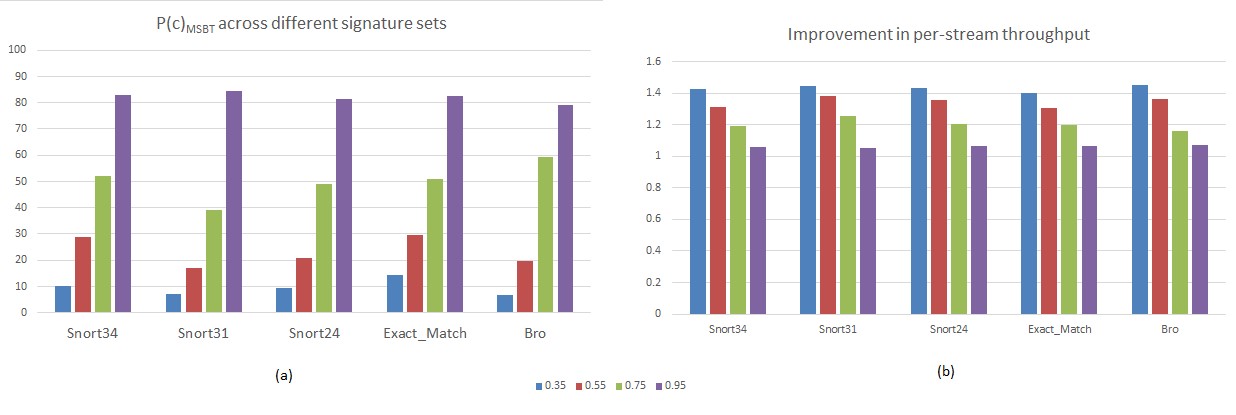
Figure 15(a) shows the statistics of the number of transitions fetched from the third stage in the case of MSBT as a percentage of total transition fetches, considering traffic traces with various levels of maliciousness. As the probability of maliciousness increases with different character traces, it can be clearly seen that more transitions are fetched from the third functional stage. This can be attributed to two reasons. Firstly, as the maliciousness level in the traces increases, the states which are at higher depths are visited, where the depth of a state refers to the number of positive character matches in a signature. The states which are visited in these cases are traversed if and only if a sequence of positive character matches leads to it. Secondly, only a very small portion of the states are the leader states, while the majority of states are member states after the state grouping process. In the case of the traces with higher maliciousness levels, the probability that the states traversed are member states is very high. The transitions which lead to the state at a higher depth are generally distinct and cannot be compressed. Thus, these transitions will belong to the member states which remain uncompressed, resulting in more transitions fetched from the third stage. Figure 16(a) shows a similar comparison in the case of LSCT and, even at the lowest maliciousness level, which is 0.35, the percentage of transitions fetched from the third functional stage is much higher when compared with MSBT. The compressed transition is fetched from the second stage if and only if the transition is the most repeated transition in the group. Those leader transitions which are different from the most repeated transition are also fetched from the third stage on top of all the member transitions which are fetched. These transitions are directly responsible for the difference in the access patterns in comparison to MSBT.

Table 6. Summary of results after injecting 1MB of byte sequence into the MSBT, the LSCT and the DFA

Figure 15. Statistics of transition fetch from the third functional stage in MSBT decompression system and the effective improvement in throughput.

Figure 16. Statistics of transition fetch from the third functional stage in LSCT-based decompression system and the effective improvement in throughput.

Figure 15(b) and Figure 16(b), respectively, shows the improvement in the per-stream throughput that can be achieved in the worst-case scenarios based on the relationship established in the previous sections. It is assumed that it takes two clock cycles to fetch the compressed state transition from the second stage, while it takes three clock cycles to fetch the compressed transition from the third stage. Based on this assumption, the improvement in the per-stream throughput is calculated based on (8) and (9), as shown in Figure 15(b) and Figure 16(b). As the level of maliciousness increases in the traffic, more transitions are fetched from the third functional stage, which reduces the per-stream throughput in the worst-case scenarios. In the case of lower levels of maliciousness, the per-stream throughput that can be achieved in the case of LSCT is less than for MSBT, as the probability of a transition fetch from the third functional stage is higher in LSCT. The difference in the throughput gradually reduces as the levels of maliciousness increase, due to the distribution of the compressed transitions. According to Michela et al. (2008), traffic traces with the highest maliciousness levels are not a common occurrence in network traffic traces. So, with low levels of maliciousness, MSBT can be used to achieve better signature matching throughput than LSCT. By assigning the next state directly from the second stage, the per-stream signature matching throughput can be increased by a factor of 1.2 to 1.4 times in the case of the MSBT and the LSCT, as shown in Figure 15(b) and Figure 16(b), respectively.

7. Conclusion

Hardware acceleration of signature matching is a key requirement to perform deep packet inspection at line rates. The signatures which are used for DPI are converted into the DFA to perform signature matching in linear time, while the storage inefficiency associated with the automata is addressed through various transition and state compression algorithms. Bitmap-based transition compression techniques enable hardware acceleration of transition decompression, in turn allowing the signature matching function to be performed in a dedicated hardware accelerator. State-of-the-art bitmap-based transition compression techniques do not efficiently compress the DFA. Addressing this problem, Subramanian et al. (2016) proposed two bitmap-based transition compression techniques to achieve transition compression rates of the order of over 98%. The transition decompression through the proposed techniques is performed in a hardware accelerator so that the signature matching can be performed at line rates. The fundamental building blocks of the hardware accelerator performing the transition decompression corresponding to these techniques were first proposed in this article. Furthermore, a software model corresponding to the decompression engines was designed and verified to validate the proposed compression methods. The functionality of the decompression engines was verified by injecting multiple 1 MB streams of bytes of different levels of maliciousness, across different signature sets, into the software models and the DFA. The identical signature matching results further validated the functional correctness of the proposed compression methods. Furthermore, a theoretical relationship was established between the signature matching throughput achieved through these systems and the number of pipeline stages required by the hardware accelerator to perform the transition decompression. Based on this analysis, further optimization methods were proposed to improve the per-stream signature matching throughput. Experimental evaluations further showed that the proposed optimizations improve the per-stream signature matching throughput by a factor of 1.2x to 1.4x in comparison to the throughput that is achieved without the optimizations.

Acknowledgement

The authors wish to thank Dharmesh Shah for his valuable feedback on this manuscript.

References

Basu, A; Narlikar, G. 2005. ‘Fast incremental updates for pipelined forwarding engines’. IEEE/ACM Transactions on Networking, 690-703.

Becchi, M. 2016. Regular Expression Processor. Retrieved from http://regex.wustl.edu/

Becchi, M; Crowley, P. 2007a. ‘An improved algorithm to accelerate regular expression evaluation’. 3rd ACM/IEEE Symposium on Architecture for networking and communications systems (pp. 145-154). Florida: ACM.

Becchi, M; Crowley, P. 2007b. ‘A hybrid finite automaton for practical deep packet inspection’. CoNEXT '07, Proceedings of the 2007 ACM CoNEXT conference. New York.

Becchi, M; Crowley, P. 2013. ‘A-DFA: A Time- and Space-Efficient DFA Compression Algorithm’. ACM Transactions on Architecture and Code Optimization, 4:1-4:26.

Chen, X; Jones, B; Becchi, M; Wolf, T. 2016. ‘Picking Pesky Parameters: Optimizing Regular Expression Matching in Practice’, IEEE Transactions on Parallel and Distributed Systems, 27 (5), May, pp. 1430-1442.

Cong, L; Yan, P; Ai, C; Jie, W. 2014. ‘A DFA with Extended Character-Set for Fast Deep Packet Inspection’. IEEE Transactions on Computers, 1925-1936.

Cormen, TH; Leiserson, CE; Rivest, RL; Stein, C. 2009. Introduction to Algorithms, Third Edition. MIT Press.

Ficara, D; Giordano, S; Procissi, G; Vitucci, F; Antichi, G; Pietro, AD. 2008. ‘An improved DFA for fast regular expression matching’. ACM SIGCOMM Computer Communication Review, 38(5), 29-40.

Handley, M; Paxson, V; Kreibich, C. 2001. ‘Network Intrusion Detection: Evasion, Traffic Normalization, and End-to-End Protocol Semantics’. Proceedings of the 10th USENIX Symposium. Washington D.C.

Holcomb, J. 2016. securityevaluators.com. Retrieved 26 March 2016 from https://security‌evaluators.com/knowledge/presentations/soho_defcon21.pdf

John, EH; Rajeev, M; Ullman, JD. 2007. Introduction to Automata Theory, Languages, and Computation, 3rd Edition. Pearson.

Kumar, S; Dharmapurikar, S; Yu, F; Crowley, P; Turner, J. 2006. ‘Algorithms to accelerate multiple regular expressions matching for deep packet inspection’. ACM SIGCOMM. New York.

Lunteren, JV; Guanella, A. 2012. ‘Hardware-accelerated regular expression matching at multiple tens of Gb/s’. INFOCOM, 2012 Proceedings IEEE. Orlando.

Michela, B; Mark, F; Patrick, C. 2008. ‘A workload for evaluating deep packet inspection architectures’. IEEE International Symposium on Workload Characterization, 2008. IISWC 2008 (pp. 79-89).

Nourani, M; P.Katta. 2007. ‘Bloom Filter Accelerator for String Matching’. Proc. ICCCN (pp. 185-190). Honolulu.

Paxson, V. 1999. ‘Bro: a system for detecting network intruders in real-time’. Computer Networks: The International Journal of Computer and Telecommunications Networking, 2435-2463. Retrieved from http://www.bro-ids.org/

Qi, Y; Wang, K; Fong, J; Xue, Y; Li, J; Jiang, W; Prasanna, V. 2011. ‘FEACAN: Front-end acceleration for content-aware network processing’. INFOCOM, 2011 Proceedings IEEE. Shanghai.

Rafael, A; Stenio, F; Djamel, S; Judith, K; Géza, S. 2012. ‘Deterministic Finite Automaton for scalable traffic identification: The power of compressing by range’. Network Operations and Management Symposium. IEEE.

Rafael, A; Stenio, F; Djamel, S; Judith, K; Géza, S. 2015. ‘Design and optimizations for efficient regular expression matching in DPI systems’. Computer Communications, 103-120.

Rajaraman, R; Sanu, M; Vasantha, E; Ram, K; Shay, G. 2008. ‘A 2.1 GHz 6.5 mW 64-bit Unified PopCount/BitScan Datapath Unit for 65 nm High-Performance Microprocessor Execution Cores’. 21st International Conference on VLSI Design (VLSID 2008). IEEE.

Ramanarayanan, R; Mathew, SK; Krishnamurthy, RK; Gueron, S; Erraguntla, VK. 2012. US Patent No. 8214414: Combined set bit count and detector logic.

Roesch, M. 1999. ‘Snort - Lightweight Intrusion Detection for Networks’. Proceedings of the 13th USENIX conference on System Administration (pp. 229-238). Washington. Retrieved from http://www.snort.org

Sappington, B. 2016. Parks Associates. Retrieved from http://www.jungo.com/wp-content/uploads/Jungo%20WP_CiscoUpdate3_3-11-13.pdf

Smith, R; Estan, C; Jha, S; Kong, S. 2008. ‘Deflating the big bang: fast and scalable deep packet inspection with extended finite automata’. Proceedings of the ACM SIGCOMM 2008 conference on Data communication. New York.

Song, H; Sproull, T; Attig, M; Lockwood, J. 2005. ‘Snort Offloader: A Reconfigurable Hardware NIDS Filter’. Proceedings of Field Programmable Logic and Applications.

Subramanian, SS; Lin, P; Herkersdorf, A. 2014. ‘Deep packet inspection in residential gateways and routers Issues and challenges’. 14th International Symposium on Integrated Circuits (ISIC). Singapore.

Subramanian, SS; Lin, P; Herkersdorf, A; Wild, T. 2016. ‘Hardware acceleration of signature matching through multi-layer transition bit masking’. International Telecommunication Networks and Applications Conference. Dunedin: IEEE.

Team Cymru Threat Intelligence Group. 2016. ‘SOHO Pharming’. Retrieved 26 March 2016, from https://www.doc.ic.ac.uk/~maffeis/331/TeamCymruSOHOPharming.pdf

Tuck, N; Sherwood, T; Calder, B; Varghese, G. 2004. ‘Deterministic memory-efficient string matching algorithms for intrusion detection’. INFOCOM 2004. Twenty-third Annual Joint Conference of the IEEE Computer and Communications Societies. Hong Kong.

Wang, K; Qi, Y; Xue, Y; Li, J. 2011. ‘Reorganized and Compact DFA for Efficient Regular Expression Matching’. 2011 IEEE International Conference on Communications. Kyoto.

Wesley, M; Stenio, F; Rafael, A; Djamel, S; Judith, K; Szabó, G. 2012. ‘Benchmarking of compressed DFAs for traffic identification: Decoupling data structures from models’. IEEE Global Communications Conference. IEEE.

Xu, C; Chen, S; Su, J; Yiu, SM; Hui, LC. 2016. ‘A Survey on Regular Expression Matching for Deep Packet Inspection: Applications, Algorithms, and Hardware Platforms’. IEEE Communications Surveys & Tutorials, 18(4).

Yang, X; Junchen, J; Rihua, W; Yang, S; H. Jonathan, C. 2014. ‘TFA: A Tunable Finite Automaton for Pattern Matching in Network Intrusion Detection Systems’. IEEE Journal on Selected Areas in Communications, 1810-1821.

Yu, F; Chen, Z; Diao, Y; Lakshman, T; Katz, R. H. 2006. ‘Fast and memory-efficient regular expression matching for deep packet inspection’. Proceedings of the 2006 ACM/IEEE symposium on Architecture for networking and communications systems. New York.

Yu, X; Lin, B; Becchi, M. 2014. ‘Revisiting State Blow-Up: Automatically Building Augmented-FA While Preserving Functional Equivalence’. IEEE Journal on Selected Areas in Communications, 32(10), 1822-1833.

Zeydel, BR; Baran, D; Oklobdzija, VG. 2010. ‘Energy-Efficient Design Methodologies: High-Performance VLSI Adders’. IEEE Journal of Solid-State Circuits, 1220-1233.