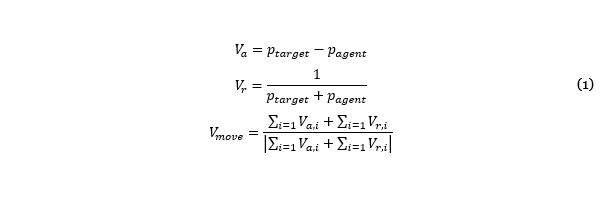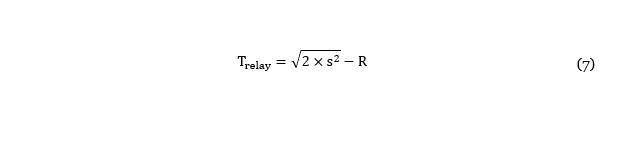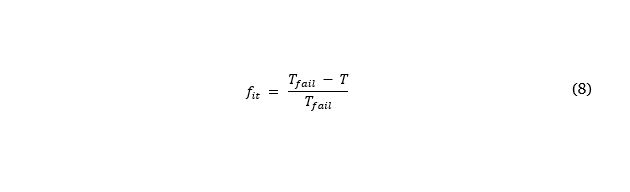Introduction

Augmenting Mobile ad hoc network (MANET) topologies with unmanned autonomous vehicles has recently been investigated in the literature (Llorca, Milner & Davis, 2007; Fraser & Hunjet, 2016; Zhang & Quilling, 2011; Dixon & Frew, 2007; Henkel & Brown, 2008; Zhao, Ammar & Zegura, 2004; Zhao & Ammar, 2003). The techniques found include: distributed optimisation (to increase network survivability); relay chaining Unmanned Aerial Vehicles (UAVs); and data ferrying when connectivity cannot be maintained. Each of these techniques addresses the networking problem well in its specific context, but does not operate well in alternative environments; e.g. a distributed optimisation method for increasing survivability is not applicable to a disconnected network where data ferrying is necessary. Such techniques can be considered expert-system-type approaches and suffer from the no free lunch dilemma (Wolpert & Macready, 1997), in which any one method will solve some problems well but perform poorly in others. This issue is not confined to the communications domain, existing in many disciplines. Hyper-heuristic (HH) approaches, which allow for generation and real-time selection of heuristics to address a given problem space, have recently been proposed as a method to address this issue (Poli & Graff, 2009).

In this paper, we examine mobile networking devices for sparse communication. Within this domain UAVs can aid in data communication between two nodes via relay or ferry methods, with the former having lower packet delays, and the latter spanning greater distances. Prior works (Henkel & Brown, 2008) have addressed communications using one or the other. However, for an agent to make this decision autonomously, apt network information and prior human control must define the network circumstances for each method to be used. This is time consuming and requires extensive testing. Finally, if a collection of agents select from a discrete set of transfer methods, the group will require unification of action selection via a plan consensus, such as auctioning (Pourpanah, Tan, Lim & Mohamad-Saleh, 2017) or voting (Valentini, Ferrante, Hamann & Dorigo, 2015). This will, in turn, require a high level of shared environment knowledge, as agents must make an educated assessment. This combination of environment knowledge and action planning comes at a large inter-group communication cost, which is undesirable in restricted communication environments and is not scalable.

To counter the above issues Swarm Robotics is a growing research topic. Swarms have a basic control system which, when implemented in large groups, exhibits emergent behaviour. That is, these units can individually perform basic tasks, which collectively produce complex global results. These swarms are praised for being decentralised, robust, scalable and flexible (Brambilla, Ferrante, Birattari & Dorigo, 2013). However, standard swarm design requires detailed testing and evaluation to develop these emergent behaviours. By having the swarm learn and evolve individually it is believed the robustness and flexibility will increase, while maintaining scalability and reducing the need for manual adjustment. The main contribution of this paper is the development of a simulated learning and evolving swarm, which must transfer a number of data packets between source and sink network ‘base stations’ out of communication range with one another. A swarm of the proposed robotic agents evolves rule-sets and learns appropriate rules for transferring the time-insensitive packets via requesting transmission from the bases, transmitting amongst themselves, and moving about the environment. The novelty of this intelligent swarm is the combination of standard swarm properties with online (during operation) reinforcement learning, and offline (post-operation) heuristic evolution. To fully explore the value of this combination, evolution experiments without the learning process are also conducted.

The remainder of this paper is structured as follows: a background of UAV data transfer methods, collaborative agents, rule learning and HH is given in Related work; the swarm agent design, including agent knowledge, action processing, and learning/evolving, is presented in System design; further specifications of the communication bridging problem and reward function are presented in Application scenario; details and results of the experiments explored in this study are presented in Experiment Setup and Experimental Results; and finally the paper is concluded in Conclusion and Future Work.

Related Work

The two most popular methods in the literature of having a MANET of UAVs transfer data between geographically dispersed network nodes are relaying and ferrying.

Relaying (Llorca et al., 2007; Zhang & Quilling, 2011; Dixon & Frew, 2007; Henkel & Brown, 2008; Lee, Fekete & McLurkin, 2016; Mehrjoo, Sarrafzadeh, & Mehrjoo, 2015) sees the agent place itself between the two nodes, thus halving the transmission distance each packet must be sent per hop. A collection of units may evenly disperse about this distance, creating a multi-hop chain (Llorca et al., 2007; Dixon & Frew, 2007). However, the relay method is range-limited, based on the number of relays used. Each relay in the chain must have a receiver and sender neighbour: thus, the maximum range of the relay system is R·(k+1), where R is the stable communication range of the relays, and k is the number of relays.

The ferry method (Fraser & Hunjet, 2016; Henkel & Brown, 2008; Zhao et al., 2004) has each agent move to be in range of the transmitting device, where it collects a number of packets equal to its buffer size. The agent then physically moves toward the receiver and, upon communication-link establishment, will transfer the buffer content. In conveyor belt ferry (Henkel & Brown, 2008) each agent makes this full travel, while in Newton’s cradle (Fraser & Hunjet, 2016) each unit ferries from the closest sending neighbour to the closest receiving neighbour. This sub-method of ferrying can be seen as a hybridisation of ferry and relay, though is only one possible splicing. In general, the ferry method has much greater delay time and energy consumption, but can span much greater distances (Zhao et al., 2004).

In Henkel & Brown (2008), an adaptive agent is proposed that switches between relaying and ferrying approaches based on distance. However, the work only suggests a binary swap between the two extremes (relaying and ferrying) rather than utilising features of both. Additionally, the decision of when to switch methods must be calibrated manually in this approach.

A fleet of adaptive Unmanned Aerial Systems can be thought of as a collection of intelligent agents. The literature covers multiple philosophies for the implementation of agent coordination. We briefly describe two of these, swarming and teaming, below. Swarm agents are often very simple, as seen in Lee et al. (2016), Mendonca, Chrun, Neves & Arruda (2017) and Kanakia, Touri & Correll (2016). These agents lack object permanence via environmental modelling, often use a human-devised hard-coded action rule list, or have limited direct messaging between members. Furthermore, the actions performed by the agents are often not selected to explicitly solve a goal. Rather actions are triggered via stimuli. These stimuli-action relations are often set by humans to orchestrate a greater swarm behaviour (emergent behaviour), which leads the swarm to achieve an objective of which the agents have no understanding. Consider as an example swarm taxies (Timmis, Ismail, Bjerknes & Winfield, 2016), in which units fluctuate between travelling toward and away from the swarm centre. When a light source varies the ratios of these two actions, the swarm can drift toward an illuminated goal location without the agents directly attempting to do so.

A team of intelligent agents (Johnson, Choi, & How, 2016; Riccio, Borzi, Gemignani, & Nardi, 2016) will have a collection of independently capable agents interact. These agents often have shared operational plans and detailed environment model sharing. Some promote consensus or distributed optimisation-based methodologies (Johnson et al., 2016). Such approaches require time to reach a decision, high network bandwidth, and complex onboard computations. These methods may also be vulnerable to malicious data injection, which would confuse or stall the group (Rada-Vilela, Johnston & Zhang, 2014). Additionally, some approaches require rendezvous (Lee et al., 2016) of the agents, which creates a failure chain-reaction, as one member failing will cause rendezvous members to stall in a waiting state.

In this paper we propose the first design of a robotic agent with the strengths of both approaches, namely: the complex problem solving of team robotics; and the robustness, scalability, flexibility and decentralisation (Şahin, 2004) of swarm robotics. By using swarms with emergent behaviours, online planning is not required and the swarm is not affected by the above issues.

Machine learning (ML) is a common approach applied to complex problem-solving in the literature. Action rules are used in Markovian Decision ML, such as Monte Carlo Tree Search (Ayob & Kendall, 2003; Kao, Wu, Yen & Shan, 2013; Gelly et al., 2012) and Temporal Learning (Szepesvári, 2010). In these studies, a rule links a single state to an action, with a state fully defining all variables of the agent and observed environment at the time-step. In this paper we propose agents hold a collection of rules, with each linking a state condition and an action to perform. That is, rule p = {c,a}, where c defines only some of the variables of a full agent state, and a is a specific action from all actions, A. The rule is scored via the reward of the action.

One approach for creating these rules is heuristic generation (Løkketangen & Olsson, 2010; Keller & Poli, 2007; Bader-El-Den, Poli & Fatima, 2009; Burke, Hyde, & Kendall, 2012). In this approach the known heuristic methods, here ferrying and relaying, are broken into components. The system creates its own heuristic by randomly re-assembling these components into a set of rules. This has been noted in the literature to be much more computationally expensive than selecting from complete heuristics, though the produced heuristics can be specialised toward a problem domain (Burke et al., 2013). Additionally, the granularity of heuristic decomposition is an important consideration: large granularity will restrict the system’s flexibility, while small granularity can overly expand the search space (Bader-El-Den et al., 2009).

We argue that the combination of heuristic generation and ML provides a stable yet flexible robotic swarm, which may more expressly adapt its behaviour to solve data transfer problems.

System Design

This section presents the design of the robotic swarm unit. Each unit holds basic information about other swarm members and other devices utilised for the problem. In each time step, the swarm communicates with its peer neighbours (other swarm nodes in range) or moves about the environment.

Agent Knowledge

Unlike a collection of intelligent agents, the swarm agents of this study have limited sensing ability and shared information. Each agent is aware of its ‘neighbourhood’, i.e. all agents that are within communication range, R, at the current time step. Each neighbour advertises its relative location, including distance and angle, and if it currently holds a data packet. An agent also keeps a record of all known agents. This record consists of the known agent’s ID, its last known location, and the age of the sighting, which is incremented each time step. With this knowledge, an agent is able to plan movements in relation to others outside its communication range. This memory prevents an agent becoming stranded, should it stray out of communications range, as seen in (Timmis et al., 2016). At each time step all neighbours are added or updated to this known agent list, where newly found agents are added, and prior known agents are updated with current locations.

Also within the time step, agents request known agent data from neighbours. At the receipt of this data, an agent updates its records to reflect the most up-to-date information (consolidating the records from neighbours and itself, using the record with lowest age). This process allows a co-swarm member’s location to be promulgated through the swarm in a ‘multi-hop’, peer-to-peer fashion. This allows the swarm to make more informed decisions: note that, in the absence of this information, localised decisions are still made.

Additionally, if a known agent record states an agent should be in communications range, but the agent is not found during the neighbourhood update, it is assumed that it has moved since the known location record was made. The entry is thus removed, as it is confirmed to be no longer correct. Finally, each agent is provided with the sink device’s location, which prevents an environment searching process to be conducted at the beginning of an experiment.

Action Targeting

Using the above knowledge, an agent will perform actions in relation to fellow swarm members (SMs) and/or non-swarm devices (bases). To select the target(s) of action focus, the following filters and selectors are used: agent type, direction and position. These restrictions allow the action to be more specific in its application, and thus more complicated behaviours to be performed by the swarm. The agent type filter restricts the interactions to only SMs, only bases, or both (no filter). The direction filter restricts to only SMs/bases toward or away from the sink location (relative to planning agent’s position) or any direction. Finally, position defines the single or group of SM/bases to be used for the action. This requirement finds the member closest to the agent, second closest to the agent, furthest from the agent, SM/base closest to the sink device, all SMs/bases in communication range, or all SMs/bases in the known agent list.

With these targeting filters and selection method, an agent is able to define a collection, which may be of size one, to dictate the focus of the action execution.

Agent Mobility

The movement of agents is limited to attraction and repulsion of targetable agents in the environment (see Action Targeting). This collaborative movement planning is known as ‘virtual forces’ (Imaizumi, Murakami, & Uchimura, 2013; Vieira, Govindan, & Sukhatme, 2013). Using a target collection, force vectors are calculated and summed to form a single movement plan as follows:

where V_a, V_r are the attraction and repulsion force vectors, and p_target, p_agent are the locations of the respective units.

Reinforcement Learning

To learn the best actions to take in each time-step, Q-learning (Szepesvári, 2010) is utilised over the swarm operation. This learning equation is defined as

                                              Q(c_t,a) = Q_t(c_t,a)(1 − α) + α(ρ + γ·Max(Q(c_t+1,a)))                        (2)

where Q(c,a) is the quality score for rule {c,a} (condition, action), γ is the future rule discount factor, α is the learning rate, ρ is the action reward and Max(Q(c_t+1,a)) is the predicted maximum quality score of the next rule. At each time step a greedy selector is used, selecting the rule with condition c being true and the greatest Q value. Additionally, an adaptation of QS-learning (Ribeiro, Pegoraro & Reali Costa, 2002) is used to accelerate learning. QS-learning is used in Ribeiro et al. (2002) to share Q value learning with similar states. In Ribeiro et al. (2002) ‘similar’ is defined as geographically close location states. In this work conditions are explored rather than fully defining states; therefore QS-learning shares rewards with other true-condition rules which hold matching actions.

Evolution

After a set number of learning cycles, or when the objective has been completed, the learning process is ended and the higher level HH Evolution (HHE) is implemented. In this stage, each agent is judged on its contribution toward the objective(s). Any agent that contributed below the mean has its rule-set mutated. This requirement prevents the HHE adjusting relatively functional agents.

To determine the quality of each rule, during the simulation a secondary score, HHScore, is assigned to each rule, in each agent, similar to the Q value. This HHScore uses limited back-propagation learning, inspired by TD(λ) (Szepesvári, 2010). In this study, BP_depth is a past-rule depth to back-propagate with no decay, while traditional TD(λ) back-propagates all rules explored thus far, with a learning decay rate of λ. It is seen that this adaptation reduces required memory storage of each agent, as only the last BP_depth rules must be stored. It is also seen that equivalent results will be produced when λ^BPdepth → 0. In this study the HHscore value of the last BP_depth rules is adjusted via

                                                                  HHscore_t = HHScore_t−1 + |ρ|/ρ                               (3)

This inclusion of HHscore allows the offline evolution to find the best over-all rules, rather than only the best at the end of the simulation. As an example of this HHScore requirement, a ‘collect from base station’ rule may be Q-value-positive at the start of the simulation, when the action is required; but the Q-value will become low at the end of the simulation, when there are no packets to collect. The HHscore of this rule will not so rapidly decrease, and will be reported to the HH evolution as a quality rule.

During the mutation of an agent’s rule-set, the rule with lowest HHscore randomly has its condition or action regenerated.

After these changes are made all agents have rule HHscores and Q-values reset and the operation is restarted, with the agents at their original geographical position.

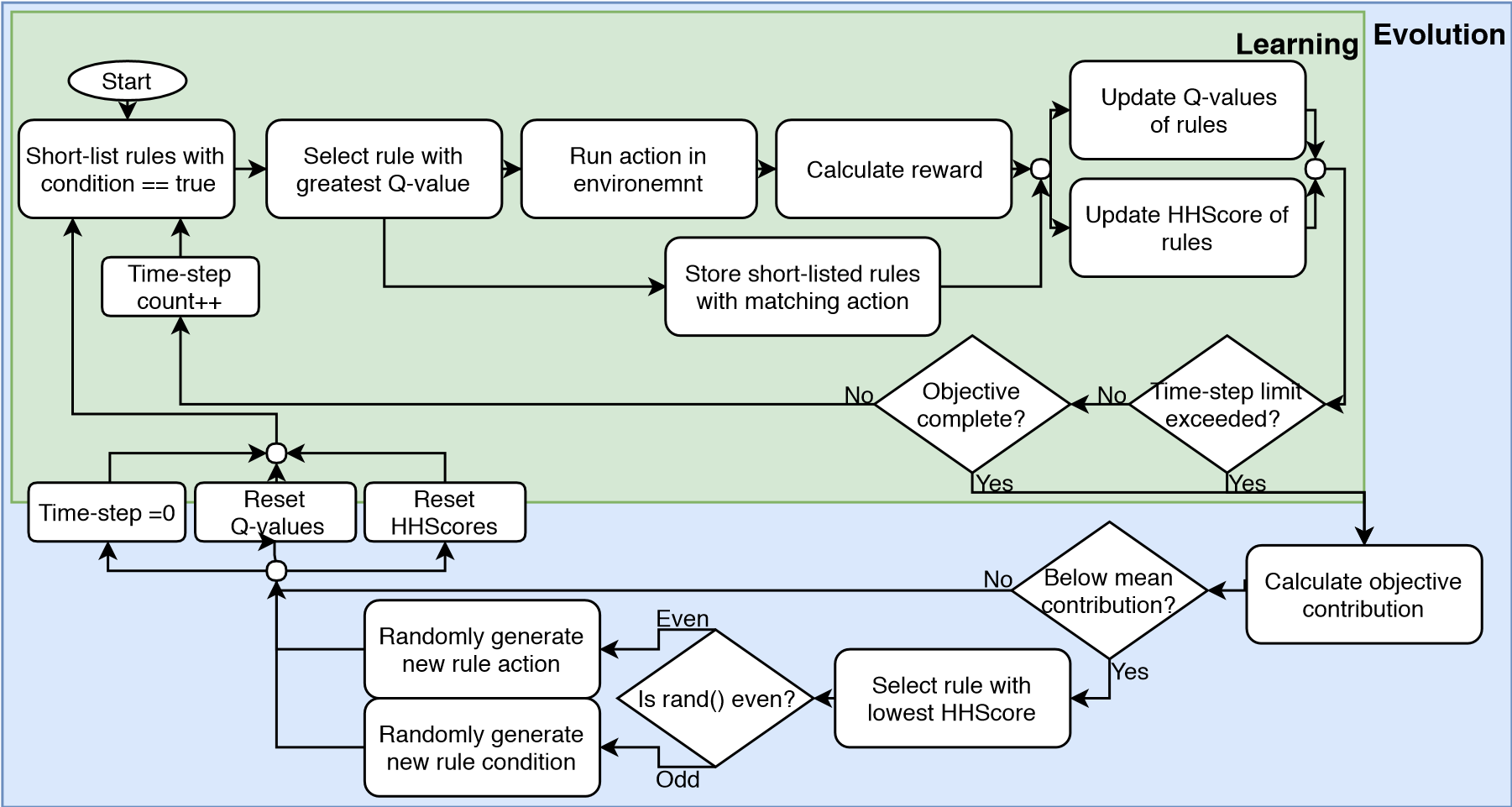
To summarise, the Q-learning is a short-term, online learning process, which is used for in-field action control. The HHE is the long-term improvement, which shifts the available rules towards an optimal set in the heuristic space. Figure 1 shows the overall cycle of these two iterative processes.

Figure 1. Flow diagram of both iterative processes

Application scenario

The Multi-Agent Simulator of Networks (MASON) (Laboratory & the GMU Center for Social Complexity, 2017) Java-based discrete event simulator is used to create an experimental simulation environment to test the proposed approach. As presented in the Introduction section, the swarm agents are tasked with moving data-packets from a source base to a sink base. As such, agents can only send and receive packets from neighbouring units. Furthermore, for this experiment, only one copy of a packet exists at a time, i.e. broadcasting and network flooding are not explored. This constraint was added to reduce the network load, allowing the swarm to operate in communication-restricted environments. It should be noted, however, that this restriction will result in the permanent loss of data if a swarm individual holding the data is lost. Finally, a simplistic network model is used, assuming symmetrical wireless range.

Wireless range equation

To model the communication range between all nodes, the log-distance path loss model (Rappaport, 1996) is used. The propagation path loss (in dBm) between nodes is

                                                    P_loss,db(d) = P_loss(d₀) + 10l·log(d/d₀) + X(σ)_db                       (4)

where P_loss,db(d₀) is the loss at a reference distance, l is the path loss exponent and X(σ)_db is a Gaussian random variable, with standard deviation σ. For this study, a Wifly radio module is modelled (Networks, 2011). This unit has an effective isotropic radiated power (EIRP) of +12dBm and a signal strength receiving threshold of -83dbm. This yields a link budget of 95dB.

In this initial testing, the fading variable, X(σ) is set to zero, allowing for agent learning and evolving to be explored in a stable environment. A high path loss exponent value of 5 is used, representing the agents operating in an urban environment with high specular reflection (Faria, 2005).

Reward calculation

In this application the action reward, ρ in (2), is found each time-step via the sum of relevant packet scores. A packet’s score, f_p, at each time-step is defined as

                                                                          fp = dist_{sink,t−1}− dist_sink,t                         (5)

where dist_sink,t is the physical distance from the sink device at time-step t. This is inspired by geographical routing (Ghafoor, Lloret, Sadiq & Mohammed, 2014).

This equation scores the packet via the improvement in distance from the sink device within the time-step.

Each action reward is the sum of an action-cost and rewards from three collections of packets: those held by the agent throughout the time-step (ph); those newly received by the agent in the time step (pr); and those sent by the agent in the time step (ps). Additionally, to prevent over scoring, a symmetric logarithmic function is performed on the packet rewards. The action’s fitness, or reward, thus becomes:

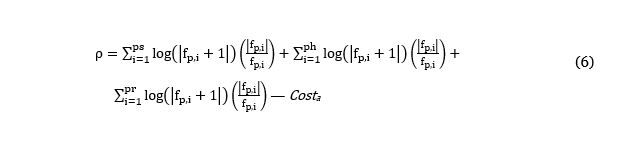
This fitness function requires the packet duplication-free restriction: should packet broadcasting be permitted, it is theorised all agents will learn and evolve rules to maximise ps based scores. This will be optimal locally but globally will congest the network.By scoring for sent packets the agent is encouraged to transfer packets onward; by scoring held packets, the agent is encouraged to move toward the sink device; by scoring received packets the agent is encouraged to position itself where other agents may transmit to it. It may be noted that a packet transfer will lead to two rewards: one agent is rewarded for sending, the other for receiving. This scoring was implemented to encourage cooperation between swarm members. Finally, by adding an action cost a simulated energy conservation is implemented into the agent learning. In this study, movement actions will have a greater cost than transmission actions, which represents the battery consumption difference between making a fixed-altitude forward motion with a quadcopter and operating a low-range radio adaptor.

Experiment Setup

Behaviour Evolution

In the first experiment, the ability of the swarm to evolve new behaviours to suit different environments is explored. Therefore, the base units are statically placed at different distances apart: 95, 113 and 128 distance-units. In each of these base deployments, three levels of background RF noise are explored, giving P_loss(d₀) values of: 45 dB, 36 dB and 30 dB. Given the receiver sensitivity of -83dBm and the path loss model described by (4), this yields a maximum reception range, R, of 10, 15 and 20 units respectively.

These 9 experiments test the ability of the swarm to evolve and learn behaviours appropriate for the given task.

Mid-flight failure

In the second experiment, the ability of the learning and HHE to cope with losses is tested by the periodic removal of agents during the simulation. This removal emulates the stochastic and error-prone environments these agents may be exposed to, including hardware failure, such as batteries or motors, and unknown hostile activity. When an agent is ‘removed’ it is not able to receive or transmit packets, nor able to announce its presence for neighbourhood updating. However, other agents do not automatically remove the lost agent from their ‘known agent’ lists unless the lost agent’s absence is observed, as discussed in subsection Agent Knowledge.

When an agent is lost, two methods are explored for re-populating the swarm: mid-mission and post-mission re-population. It is assumed an endless supply of agents are held for re-population. In the former method, the unit deployment system is assumed to be fully aware of the environment and activates new units, with newly generated rule-sets, one time-step after a unit is removed. The latter method, post-mission re-population, has the swarm complete the operation with the reduced swarm size; and only after the evolution process, when the agents are being re-deployed, will new members be introduced. For this latter re-population method, two sub-approaches are explored: one in which the new agents generate new rule-sets; and the other with agents being implemented with the rule-sets of the lost agents, or cloning the lost agent.

Results from this testing aim to explore both the swarm’s resilience to minor failure and the ability of the evolutionary algorithm to adjust from a major failure.

In all the tests, R is set to 15, the distance between bases is 113, and a constant agent removal interval of 3,000 time-steps is used.

Scalability

As an exploration of the scalability of the swarm, that is, the ability to operate effectively irrespective of the number of agents implemented in the swarm, the third experiment explores a range of base separation distances the swarm must cover, with a range of swarm members. This exploration also furthers the examination of the swarm to adjust its behaviour for a given environment. The swarm sizes explored are between 2 and 30 swarm members, in increments of 2. The distance the swarm must transmit data is based on the equal shifting of both the latitude and longitude of one base agent. This gives total base distances via the hypotenuse of the isosceles right triangle with sides, s, between 10 and 490, with increments as seen fit. These swarm and environment ranges are seen to adequately demonstrate the scalability of the swarm, without introducing excessive computation requirements. In this experiment the background RF noise is set to a constant value, resulting in R=15 units for communication range between agents.

As a comparison for this exploration, a theoretical, static-behaving relay swarm is examined. Each static swarm member has an allocated fellow swarm member or base to transmit to, and will only move to reach communication with this device. As such, the execution time is the maximum agent movement time, along with the transmission time, which is directly proportional to the number of packets, which in this study is 20. This leads to a theoretical execution time of

Learning contribution

The final exploration of this study validates the inclusion of the learning algorithm in the autonomous behaviour process. In this study, the swarm agents continue to examine rule value via the HHScore parameter, and undergo HHE. However, in each time-step, rather than selecting rules via the highest Q-score, agents use a random selection of the rules with true conditions. This increases the responsibility of the evolution process to create rule-sets that have specific, appropriate rules for all states observed.

For this test-set, only R = 15 is explored, for the three base distances, 95, 113 and 128.

Settings

In all the tests of this exploration, the Q-learning variables (α and γ) are set to values of 0.1 and 0.9, respectively. γ is set as seen in literature (Ribeiro et al., 2002), while α is tuned for this study. Online learning rate adjustment is not used in this work, as each problem instance is seen to have a different optimal learning rate, meaning the required exploration would be too computationally expensive. As such, the HHE incorporated this static learning into the problem in which it is adapting. The BP_depth value is set to 10 after exploratory testing. The action cost penalties are 0.9 for movement, and 0.1 for all other actions. The learning and evolution process is repeated as many times as possible within 1,000,000 time-steps, a value chosen to ensure reasonable simulation time.

For this study, the swarm is tasked with transferring 20 packets within the time limit, T_fail, which for the majority of tests is set to 20,000 time-steps. This limit is imposed to have solutions created of meaningful value and to force a minimum number of evolution steps over the trial. For the scalability experiment, T_fail is set to 50,000 to accommodate the larger environment navigation time.

For all results, the fitness of each evolved solution is measured via

where T is the time taken to transfer all packets.

Each agent holds 50 rules. Initially 12 of these are human designed, inspired from ferrying and relaying heuristics. Some example ferry rules are shown in Algorithm 1. The other 38 rules are randomly generated at agent initialisation. The random generation process uses a grammar with a granularity high enough for a large range of rules to be created, without the evolution process being stalled by an overly broad behaviour space.

In regard to the evolutionary search method, an Adaptive Iteration Limited Threshold Accepting (AILTA) (Misir, Verbeeck, De Causmaecker & Berghe, 2010) move acceptance is used for local-optimal solution exploration.

In all experiments, except scalability, a swarm of 8 units is implemented.

Furthermore, in most experiments, each simulation is run 30 times with different rule generation seeds. This prevents statistical anomalies and provides adequate data for a 90% confidence value to be determined. For scalability, only one simulation is run per swarm scale, per environment size, due to the high volume of simulations required for the experiment.

Experimental Results

Behaviour Evolution

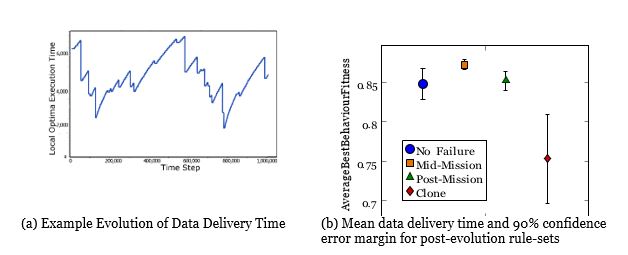
In Figure 2a an example of the evolution process for the first test case is shown. Each change in the local optima data delivery time (vertical axis) indicates a full simulation run result. From time 0 to 400k new local optima are found approximately every 100k time steps. Then at 500k a local optimum is found that cannot be surpassed. The system continues to explore without better results, increasing the acceptable threshold to escape this local optimum with AILTA. At 820k the cusp of a new solution-space optimal area is found, which leads the evolution to the best-found rule-set at 910k. This shows that throughout the one million time-steps the system is always evolving and improving, rather than stagnating at local optima.

Figure 2. First test set, exploring three swarm unit communication ranges, and three base distances (‘BaseSpan’)

In Figure 2b the mean best fitness of all 30 evolution executions is shown for the three RF noise levels and three static base positions, along with 90% confidence intervals. In addition, the red bar shows the fail-rate (right vertical axis) where failure is defined as the system not evolving a rule-set which can transfer all packets within the time limit.

As can be seen for the more challenging scenario instances, with smaller R values and greater base separation, the system not only takes longer, on average, to complete the data transfer but the confidence intervals are increased. The former of these issues is expected, as more time-consuming methods must be used to achieve the objectives. The latter issue indicates that the harder the problem instance, the more susceptible the swarm is to the rule generator seed. This leads to larger variations in the solutions found.

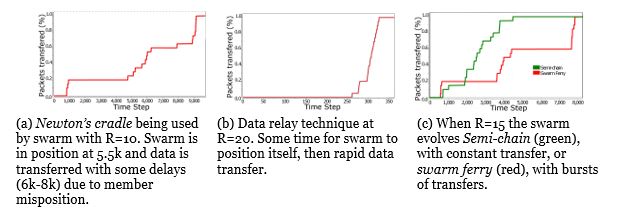
Figure 3. Packet transfer vs time step for post-evolution solutions

In Figure 3 the packet transfer process can be observed by recording the percent of packets delivered to the sink base over time-steps. These recordings are taken from the post-evolved rule-sets with noteworthy emergent behaviours. In low communication range tests with a short travel distance (when bases are 95 units apart), Newton’s cradle transfer predominantly emerged, Figure 3a, while larger communication ranges (R=20) allow for relay chains to be established in all base separations, Figure 3b. The most variant cases are when the two bases are at maximum separation (128 units), with communication range, R, of 10 or 15. In these tests, relaying is often not achievable, while standard ferrying is too time-consuming, and is avoided due to high action costs, thus different ferry-relay hybridisations are evolved, Figure 3c. These data transfer methods have not been found in the literature and are thus labelled and discussed.

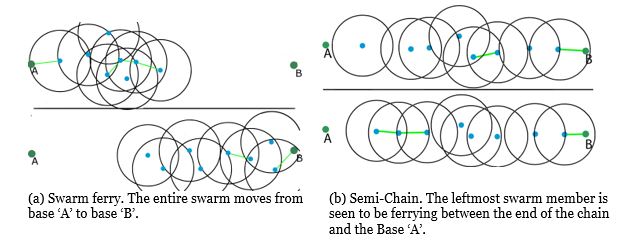
Figure 4. Swarm visual representation. (Blue circles being the swarm units, black rings being the unit’s communication range, larger green circles are base devices, lines between the units/devices are packet transfers.)

In some cases, swarm ferrying is evolved. This has the swarm as a whole move from source to sink, while maintaining communication range with one another. When one agent (the source relay) is by the source, it relays data throughout the swarm until all agents have full buffers. The swarm then taxis toward the sink and, upon one agent making contact, the data is relayed through this agent. The swarm as a whole thus has a range of (R, R×(swarmSize+1)); therefore units have less travel time than a full ferry process. This method is visualised in Figure 4a.

The second observed behaviour is the semi-chain. In this method the swarm builds relay chains starting at the sink, source or both. When the swarm size is not great enough to finish the chain, or some members of the swarm fail to fully extend the chain, the remaining distance is covered by one or two units ferrying the distance. This is shown in Figure 4b. From these diverse strategies being formed by the swarm evolution, it can be seen that the desired flexibility of this system is being achieved.

Some post-evolution, machine-generated rules, which were utilised by specific agents in the swarm ferrying behaviour, are listed in Algorithm 2 and 3. These rules are more specialised to a specific role within the swarm, which shows that HHE encourages heterogeneity.

Mid-flight failure

The second set of testing shows not only that the introduction of unit losses has minimum effect on the delivery time, but also has a positive effect on the evolutionary process. For these tests, we would like to note our previous paper (Smith, Hunjet, Aleti & Barca, 2017) showed unit removal had a negative effect on the evolutionary process, and that Post-mission re-population outperformed Mid-mission re-population. These results have now been found to be incorrect, due to an error in re-population controls in the simulations. This paper presents the results produced after addressing said problem.

For most simulation instances the system was found to be resilient to minor losses; producing results similar to Figure 2a. However, in rare cases a major failure occurred due to specialised swarm members (see Algorithms 2 and 3) being lost. Figure 5a is an example of one such instance. As can be seen, the system is improving steadily for the first 100k steps. However, at 120k the specialised member is lost. This leads the system to fail, with small recoveries over the next 400k steps. At 600k the swarm evolution process has recovered from the loss, until 800k when a specialist is lost again. This shows that major failure of the swarm is recoverable by the HHE adjusting the swarm.

Figure 5b shows that, for the first two re-population methods, mid-mission and post-mission with new unit generation, the 90% confidence interval is improved, compared to the simulations without member failure, and the mean fitness is reduced for both methods: 0.5% for post-mission and 2.9% for mid-mission. This suggests that not only can the swarm continue to operate in smaller swarm sizes, but the increased random agent turn-over aids the evolutionary process.

Figure 5. Second test, exploring swarm units being removed and new units re-populating the swarm

The difference in data delivery time between the first two re-population methods can be attributed to mid-mission always having a swarm at full capacity, while post-mission must complete simulations with multiple agents lost. Therefore, the reduced swarm can be seen to take longer, with slower approaches, yet is still capable of completing the task.

The final test case, Clone, in which the lost agents’ rule-sets are copied in the post-mission repopulation process, shows far worse results in both confidence range and mean best-evolved behaviour fitness. This is found to be due to the evolutionary process being negatively affected by the reintroduction of behaviours not fully explored in the simulation, resulting in invalid reuse in the next iteration. It can thus be seen, by comparing the two Post-mission re-population methods, that introduction of new, unknown rule-sets is preferred over the continued, unwarranted reuse of poorly performing agents.

Scalability

Figure 6a shows the evolved fitness of the swarm as its scale is increased (horizontal) and the distance of the bases is increased (vertical). These findings show the swarm is scaling effectively, with no noted reduction at large swarm sizes. That is, even with 30 agents operating in the smallest environment, the agents do not hinder one another’s ability to aid in solving the task of data transfer.

In addition, it can be seen that in all swarm sizes explored, a gradual reduction in data transfer is observed, as all swarm sizes are evolving data ferrying behaviours where appropriate. Only when the distance becomes too great, relative to the swarm size, does a ferrying behaviour not evolve.

This ability to evolve ferrying behaviours is further shown in Figure 6b, in which the theoretical relay behaviour fitness of (7) is compared. In all swarm scales, a positive (blue) comparison is observed in s values, which prevent pure relaying but allow evolved swarms to transfer via ferrying or ferry-relay hybrid behaviours.

Figure 6. Scalability of swarm operations with 2-30 agents, in environments with side lengths and widths, s, 10-490. a) simulation fitness results, b) comparison of evolved behaviour and theoretical relay behaviour.

This figure also shows in operations with large Base Ranges, s ≥ 200, in which the swarm may potentially evolve/learn relaying behaviour, swarm scale ≥ 20, the full relay is not being autonomously coordinated and the evolved behaviour is not achieving fitness values equal to the theoretical relay results. From this, and the prior observation of limited ferry behaviour range, it can be seen that the proposed autonomous evolving and learning swarm, although performing equally or better in most ranges, currently has limitations in the size of the environment in which it operates. This limitation may be due to a reduced evolutionary process, with T_fail set to 50,000 leading to only 20 generations explored. Further exploration is thus required with greater evolution allowances.

Learning contribution

The final exploration of this study is the comparison of the swarm with and without the online, learning process being implemented during the simulation.

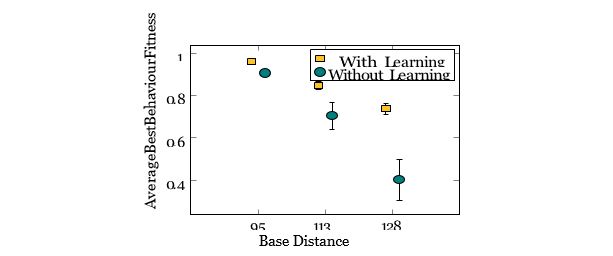
In Figure 7 it can be seen that for small base ranges, 95, where basic relaying behaviours can be achieved, the learning process contributes little to the swarm, as basic relay behaviours are evolved. However, as the base range is increased, 113 and 128, relay-ferry hybrid or full ferry behaviours are required. This leads the non-learning swarm to have far lower fitness values. This indicates that the process of adjusting the swarm behaviour to meet the requirements of the environment is heavily reliant on the learning process, particularly when non-direct actions are required: that is, actions other than moving toward the sink device and transmitting packets in the direction of the sink device.

This exploration shows that for more complex environments, the inclusion of online learning greatly increases the ability of the swarm to appropriately explore potential behaviours and adjust accordingly.

 Figure 7. Comparison of Evolving with Learning vs only Evolving

Conclusion and Future Work

This paper has explored an online-learning, offline-evolving robotic swarm system to enable communications between disconnected network nodes. The approach was validated by testing in different environments, with different rule-generator seeds; it was found that this swarming system was able to adapt its emergent behaviour to effectively transmit data between a source and a sink node. Furthermore, Figure 2a and section Learning contribution show both the evolution and learning process are required for successful behaviour adoption. The swarming system is flexible, scalable and robust, evolving behaviours to best suit the environmental conditions and performing well even with the random removal of swarm members or with excessive swarm sizes.

The evolution method presented here replaces, or at least reduces, the manual heuristic development process previously required for swarm emergent behaviours to be created. This approach will thus allow a robotic swarm to be used in new environments, without expert heuristic engineers, and with a reduction in construction time. It will also allow the environment or the swarm to change between operations, with the HHE re-designing the rule-sets to maintain an effective swarm for the next operation.

Future work will introduce Gaussian variation to the propagation path loss of the communications environment, mobility to the source and sink nodes, and examine the effect on the solutions generated through variation of the cost penalties assigned to taking specific actions.

Acknowledgement

Funding for this research was provided by Cyber and Electronic Warfare Division, Defence Science and Technology Group, Commonwealth of Australia.

References

Ayob, M., & Kendall, G. (2003). A monte carlo hyper-heuristic to optimise component placement sequencing for multi head placement machine. In Proceedings of the international conference on intelligent technologies, intech (Vol. 3, pp. 132–141).

Bader-El-Den, M., Poli, R., & Fatima, S. (2009). Evolving timetabling heuristics using a grammar-based genetic programming hyper-heuristic framework. Memetic Computing, 1(3), 205–219.

Brambilla, M., Ferrante, E., Birattari, M., & Dorigo, M. (2013). Swarm robotics: a review from the swarm engineering perspective. Swarm Intelligence, 7(1), 1–41.

Burke, E. K., Gendreau, M., Hyde, M., Kendall, G., Ochoa, G., Ozcan, E., & Qu, R. (2013). Hyper-heuristics: a survey of the state of the art [Journal Article]. Journal of the Operational Research Society, 64(12), 1695-1724. doi: 10.1057/jors.2013.71

Burke, E. K., Hyde, M. R., & Kendall, G. (2012). Grammatical evolution of local search heuristics. IEEE Transactions on Evolutionary Computation, 16(3), 406–417.

Dixon, C., & Frew, E. (2007). Cooperative electronic chaining using small unmanned aircraft. In Aiaa infotech@ aerospace 2007 conference and exhibit (p. 2746).

Faria, D. B. (2005). Modeling Signal Attenuation in IEEE 802.11 Wireless LANs. Computer Science Department, Stanford University, 1.

Fraser, B., & Hunjet, R. (2016). Data ferrying in tactical networks using swarm intelligence and stigmergic coordination. In Telecommunication networks and applications conference (ITNAC), 2016 26th international (pp. 1–6).

Gelly, S., Kocsis, L., Schoenauer, M., Sebag, M., Silver, D., Szepesvári, C., & Teytaud, O. (2012). The grand challenge of computer go: Monte Carlo tree search and extensions. Communications of the ACM, 55(3), 106–113.

Ghafoor, K. Z., Lloret, J., Sadiq, A. S., & Mohammed, M. A. (2014). Improved geographical routing in vehicular ad hoc networks [Journal Article]. Wireless Personal Communications, 80(2), 785-804. doi: 10.1007/s11277-014-2041-3

Henkel, D., & Brown, T. X. (2008). Delay-tolerant communication using mobile robotic helper nodes. In Modeling and optimization in mobile, ad hoc, and wireless networks and workshops, 2008. wiopt 2008. 6th international symposium on (pp. 657–666).

Imaizumi, T., Murakami, H., & Uchimura, Y. (2013). Deployment Control of Wireless Multihop-relay Mobile Robots Based on Voronoi Partition [Journal Article]. Electrical Engineering in Japan, 184(4), 42-51. doi: 10.1002/eej.22413

Johnson, L. B., Choi, H. L., & How, J. P. (2016, Aug). The role of information assumptions in decentralized task allocation: A tutorial. IEEE Control Systems, 36(4), 45-58. doi: 10.1109/MCS.2016.2558419

Kanakia, A., Touri, B., & Correll, N. (2016). Modeling multi-robot task allocation with limited information as global game. Swarm Intelligence, 10(2), 147–160.

Kao, K.-Y., Wu, I. C., Yen, S.-J., & Shan, Y.-C. (2013). Incentive learning in monte carlo tree search [Journal Article]. IEEE Transactions on Computational Intelligence and AI in Games, 5(4), 346-352. doi: 10.1109/tciaig.2013.2248086

Keller, R. E., & Poli, R. (2007). Cost-benefit investigation of a genetic-programming hyperheuristic. In International conference on artificial evolution (evolution artificielle) (pp. 13–24).

Laboratory, G. E. C., & the GMU Center for Social Complexity. (2017). Mason homepage. Retrieved from http://cs.gmu.edu/~eclab/projects/mason/

Lee, S. K., Fekete, S. P., & McLurkin, J. (2016). Structured triangulation in multirobot systems: Coverage, patrolling, voronoi partitions, and geodesic centers [Journal Article]. The International Journal of Robotics Research, 35(10), 1234-1260. doi: 10.1177/0278364915624974

Llorca, J., Milner, S. D., & Davis, C. C. (2007). Mobility control for joint coverage-connectivity optimization in directional wireless backbone networks. In Military communications conference, 2007. milcom 2007. IEEE (pp. 1–7).

Løkketangen, A., & Olsson, R. (2010). Generating meta-heuristic optimization code using adate. Journal of Heuristics, 16(6), 911–930.

Mehrjoo, S., Sarrafzadeh, A., & Mehrjoo, M. (2015). Swarm intelligent compressive routing in wireless sensor networks. Computational Intelligence, 31(3), 513–531.

Mendonca, M., Chrun, I. R., Neves, F., & Arruda, L. V. R. (2017). A cooperative architecture for swarm robotic based on dynamic fuzzy cognitive maps [Journal Article]. Engineering Applications of Artificial Intelligence, 59, 122-132. doi: 10.1016/j.engappai.2016.12.017

Misir, M., Verbeeck, K., De Causmaecker, P., & Berghe, G. V. (2010). Hyper-heuristics with a dynamic heuristic set for the home care scheduling problem [Journal Article]. In Evolutionary computation (cec), 2010 IEEE congress on (p. 1-8). doi: 10.1109/ cec.2010.5586348

Networks, R. (2011, Aug). Rn-xv data sheet [Computer software manual]. Retrieved from https://cdn.sparkfun.com/datasheets/Wireless/WiFi/WiFly-RN-XV-DS.pdf

Poli, R., & Graff, M. (2009). There is a free lunch for hyper-heuristics, genetic programming and computer scientists. In European conference on genetic programming (pp. 195–207).

Pourpanah, F., Tan, C. J., Lim, C. P., & Mohamad-Saleh, J. (2017). A q-learning-based multi-agent system for data classification. Applied Soft Computing, 52, 519–531.

Rada-Vilela, J., Johnston, M., & Zhang, M. (2014). Deception, blindness and disorientation in particle swarm optimization applied to noisy problems. Swarm Intelligence, 8(4), 247–273.

Rappaport, T. S. (1996). Wireless communications: principles and practice (Vol. 2). Prentice Hall PTR New Jersey.

Ribeiro, C. H., Pegoraro, R., & Reali Costa, A. H. (2002). Experience generalization for concurrent reinforcement learners: the minimax-qs algorithm. In Proceedings of the first international joint conference on autonomous agents and multiagent systems: part 3 (pp. 1239–1245).

Riccio, F., Borzi, E., Gemignani, G., & Nardi, D. (2016). Multi-robot search for a moving target: Integrating world modeling, task assignment and context. In Intelligent robots and systems (iros), 2016 IEEE/rsj international conference on (pp. 1879–1886).

Şahin, E. (2004). Swarm robotics: From sources of inspiration to domains of application. In International workshop on swarm robotics (pp. 10–20).

Smith, P., Hunjet, R., Aleti, A., & Barca, J. C. (2017). Adaptive data transfer methods via policy evolution for uav swarms. In 2017 27th international telecommunication networks and applications conference (ITNAC) (pp. 1–8).

Szepesvári, C. (2010). Algorithms for reinforcement learning. Synthesis lectures on artificial intelligence and machine learning, 4(1), 1–103.

Timmis, J., Ismail, A. R., Bjerknes, J. D., & Winfield, A. F. (2016). An immune-inspired swarm aggregation algorithm for self-healing swarm robotic systems [Journal Article]. Biosystems, 146, 60-76. Retrieved from https://www.ncbi.nlm.nih.gov/pubmed/ 27178784 doi: 10.1016/j.biosystems.2016.04.001

Valentini, G., Ferrante, E., Hamann, H., & Dorigo, M. (2015). Collective decision with 100 kilobots: speed versus accuracy in binary discrimination problems [Journal Article]. Autonomous Agents and Multi-Agent Systems, 30(3), 553-580. doi: 10.1007/s10458 -015-9323-3

Vieira, M. A. M., Govindan, R., & Sukhatme, G. S. (2013). An Autonomous Wireless Networked Robotics System for Backbone Deployment in Highly-obstructed Environments [Journal Article]. Ad Hoc Networks, 11(7), 1963-1974. Retrieved from http://www.sciencedirect.com/‌science/article/pii/S1570870512001473 doi: http://dx.doi.org/10.1016/j.adhoc.2012.07.012

Wolpert, D. H., & Macready, W. G. (1997). No free lunch theorems for optimization. IEEE Transactions on Evolutionary Computation, 1(1), 67–82.

Zhang, Y., & Quilling, M. (2011). Optimal backbone generation for robotic relay networks. In Computer communications and networks (icccn), 2011 proceedings of 20th international conference on (pp. 1–6).

Zhao, W., Ammar, M., & Zegura, E. (2004). A message ferrying approach for data delivery in sparse mobile ad hoc networks. In Proceedings of the 5th ACM international symposium on mobile ad hoc networking and computing (pp. 187–198).

Zhao, W., & Ammar, M. H. (2003). Message ferrying: Proactive routing in highly partitioned wireless ad hoc networks. In Distributed computing systems, 2003. Ftdcs 2003. proceedings. the ninth IEEE workshop on future trends of (pp. 308–314).